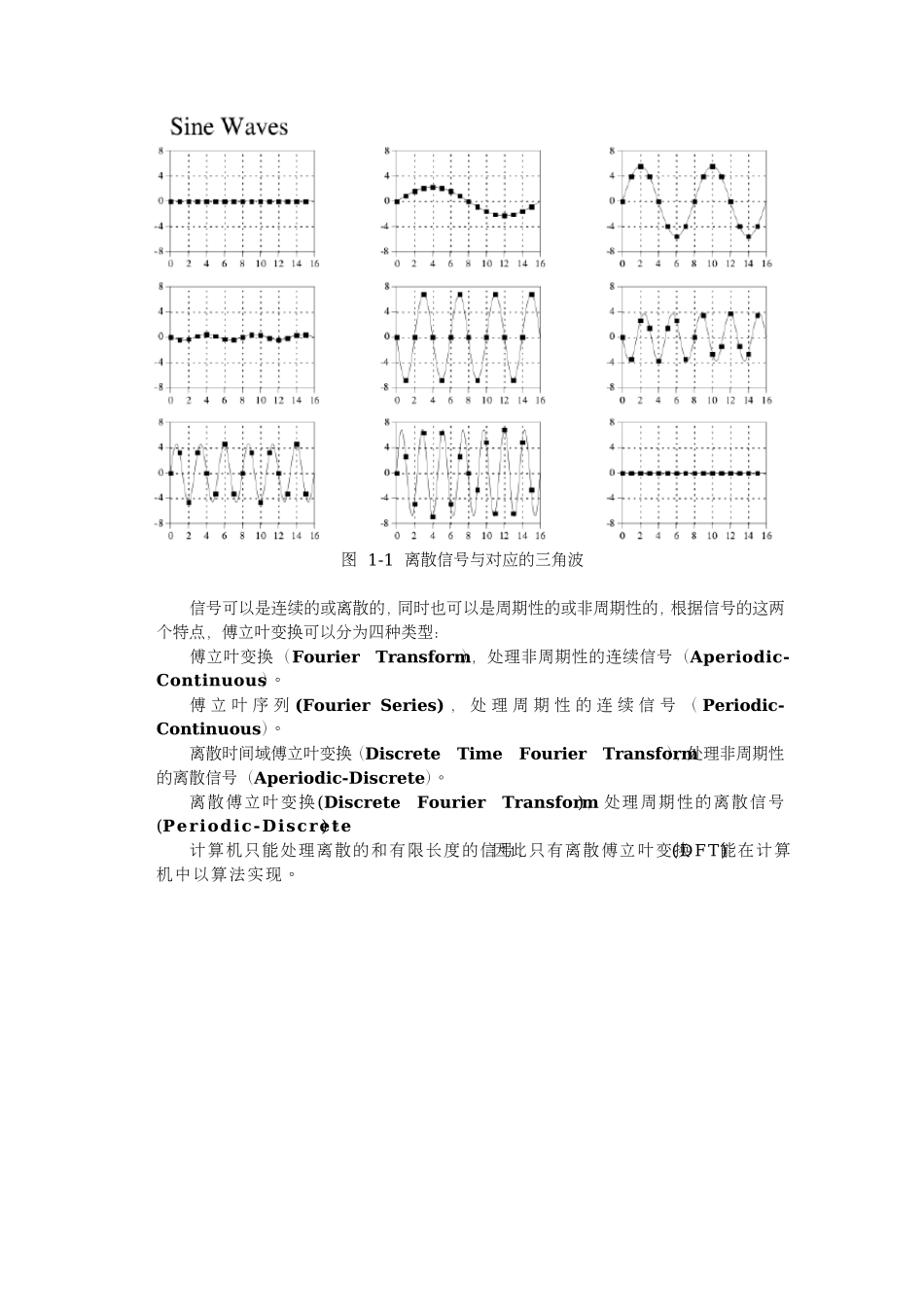
DCT 变换的原理及算法离散傅立叶变换(Discrete Fou rier Transform)离散傅立叶变换概述傅立叶分析以法国数学家和物理学家Jean Baptiste Joseph Fou rier命名,是一种将信号分解为谐波的方法。如下三图所示,一个包含 16 个点的离散信号可以用 9 个余弦和 9 个正弦波来表示。在表达任意一个离散信号时,这些三角波的周期是一定的,不同的只是振幅(amplitu de)。图 1-1 离散信号与对应的三角波信号可以是连续的或离散的,同时也可以是周期性的或非周期性的,根据信号的这两个特点,傅立叶变换可以分为四种类型:傅立叶变换(Fou rier Transform),处理非周期性的连续信号(Aperiodic-Continu ou s)。傅 立 叶 序 列 (Fou rier Series) , 处 理 周 期 性 的 连 续 信 号 ( Periodic-Continu ou s)。离散时间域傅立叶变换(Discrete Time Fou rier Transform),处理非周期性的离散信号(Aperiodic-Discrete)。离散傅立叶变换(Discrete Fou rier Transform),处理周期性的离散信号(Periodic-Discrete)。计算机只能处理离散的和有限长度的信号,因此只有离散傅立叶变换(DFT)能在计算机中以算法实现。图 1-2 四种不同类型的傅立叶分析实数离散傅立叶变换(Real DFT )的格式和表示如图1-3 所示,离散傅立叶变换将包含 N 个点的输入波转为两个包含 N/2+1 个点的输出波。输入波常被称作时间域,因为信号的波形基本上都是随时间变化,输出波常被称作频率域。时间域与频率域中存储的信息是一样的,只是表现方式不一样。将时间域转为频率域的过程叫离散傅立叶变换(DFT),将频率域转换为时间域的过程叫反变换(IDFT)。频率域可以分为两部分,实数部分 Re X[ ]和虚数部分 Im X[ ],分别存放余弦函数(Cosine)的振幅和正弦函数(Sine)的振幅。图 1-3 实数傅立叶变换示意图DFT 基函数DFT中使用的正弦和余弦函数统称为基函数(Basis Fu nction),这些三角函数的周期是固定的,变化的只是振幅。DFT 基函数的表达式:Ck[i] = cos(2πki/N)Sk[i] = sin(2πki/N)公式 1-1其中,Ck[i]和 Sk[i]表示由 N 个点组成的离散正弦曲线,i 的取值范围是张倒 N-1。k决定了曲线的周期,取值范围是 0 到 N/2。多余的系数完成DFT后,系数由原来的 N 个变为 N+2 个,似乎产生了两个多余的系数。在频率域中,的确有两个系数是多余的,它们是 Im X[0]和 Im X[n/2]。它们的存在使得...