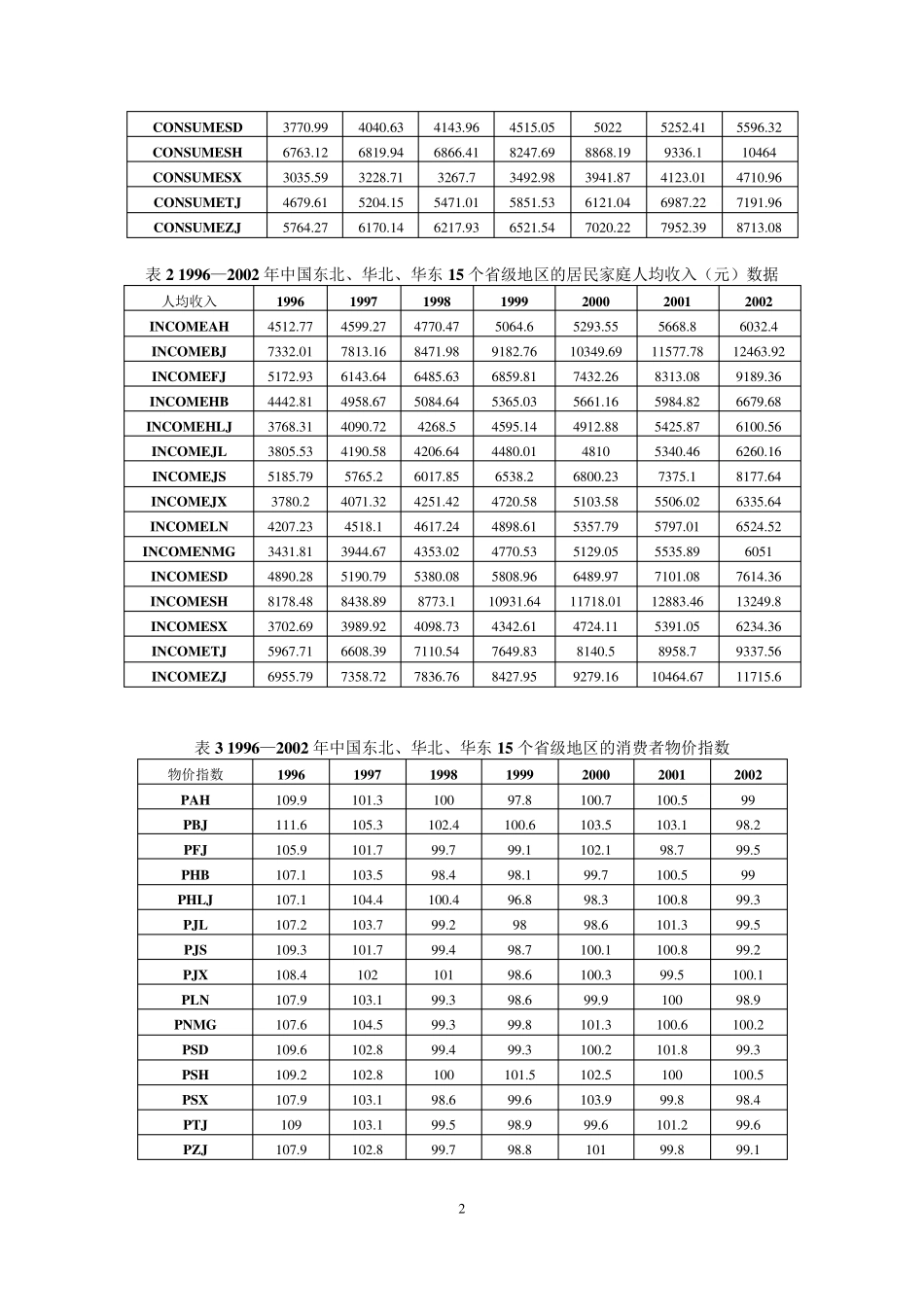
1 Eviews 面板数据之固定效应模型 在面板数据线性回归模型中,如果对于不同的截面或不同的时间序列,只是模型的截距项是不同的,而模型的斜率系数是相同的,则称此模型为固定效应模型。固定效应模型分为三类: 1.个体固定效应模型 个体固定效应模型是对于不同的纵剖面时间序列(个体)只有截距项不同的模型: 2Kitikkititkyxu (1) 从时间和个体上看,面板数据回归模型的解释变量对被解释变量的边际影响均是相同的,而且除模型的解释变量之外,影响被解释变量的其他所有(未包括在回归模型或不可观测的)确定性变量的效应只是随个体变化而不随时间变化时。 检验:采用无约束模型和有约束模型的回归残差平方和之比构造F 统计量,以检验设定个体固定效应模型的合理性。F 模型的零假设: 01231:0NH ()1(1,(1)1)(1)RRSSURSSNFF NN TKURSSNTNK RRSS 是有约束模型(即混合数据回归模型)的残差平方和,URSS 是无约束模型ANCOVA 估计的残差平方和或者LSDV 估计的残差平方和。 实践: 一、数据:已知1996—2002 年中国东北、华北、华东 15 个省级地区的居民家庭人均消费(cp ,不变价格)和人均收入(ip ,不变价格)居民,利用数据(1)建立面板数据(panel data)工作文件;(2)定义序列名并输入数据;(3)估计选择面板模型;(4)面板单位根检验。年人均消费(consu me)和人均收入(income)数据以及消费者价格指数(p)分别见表 1,2 和3。 表 1 1996—2002 年中国东北、华北、华东 15 个省级地区的居民家庭人均消费(元)数据 人均消费 1996 1997 1998 1999 2000 2001 2002 CONSU MEAH 3607.43 3693.55 3777.41 3901.81 4232.98 4517.65 4736.52 CONSU MEBJ 5729.52 6531.81 6970.83 7498.48 8493.49 8922.72 10284.6 CONSU MEFJ 4248.47 4935.95 5181.45 5266.69 5638.74 6015.11 6631.68 CONSU MEHB 3424.35 4003.71 3834.43 4026.3 4348.47 4479.75 5069.28 CONSU MEHLJ 3110.92 3213.42 3303.15 3481.74 3824.44 4192.36 4462.08 CONSU MEJL 3037.32 3408.03 3449.74 3661.68 4020.87 4337.22 4973.88 CONSU MEJS 4057.5 4533.57 4889.43 5010.91 5323.18 5532.74 6042.6 CONSU MEJX 2942.11 3199.61 3266.81 3482.33 3623.56 3894.51 4549.32 CONSU ...