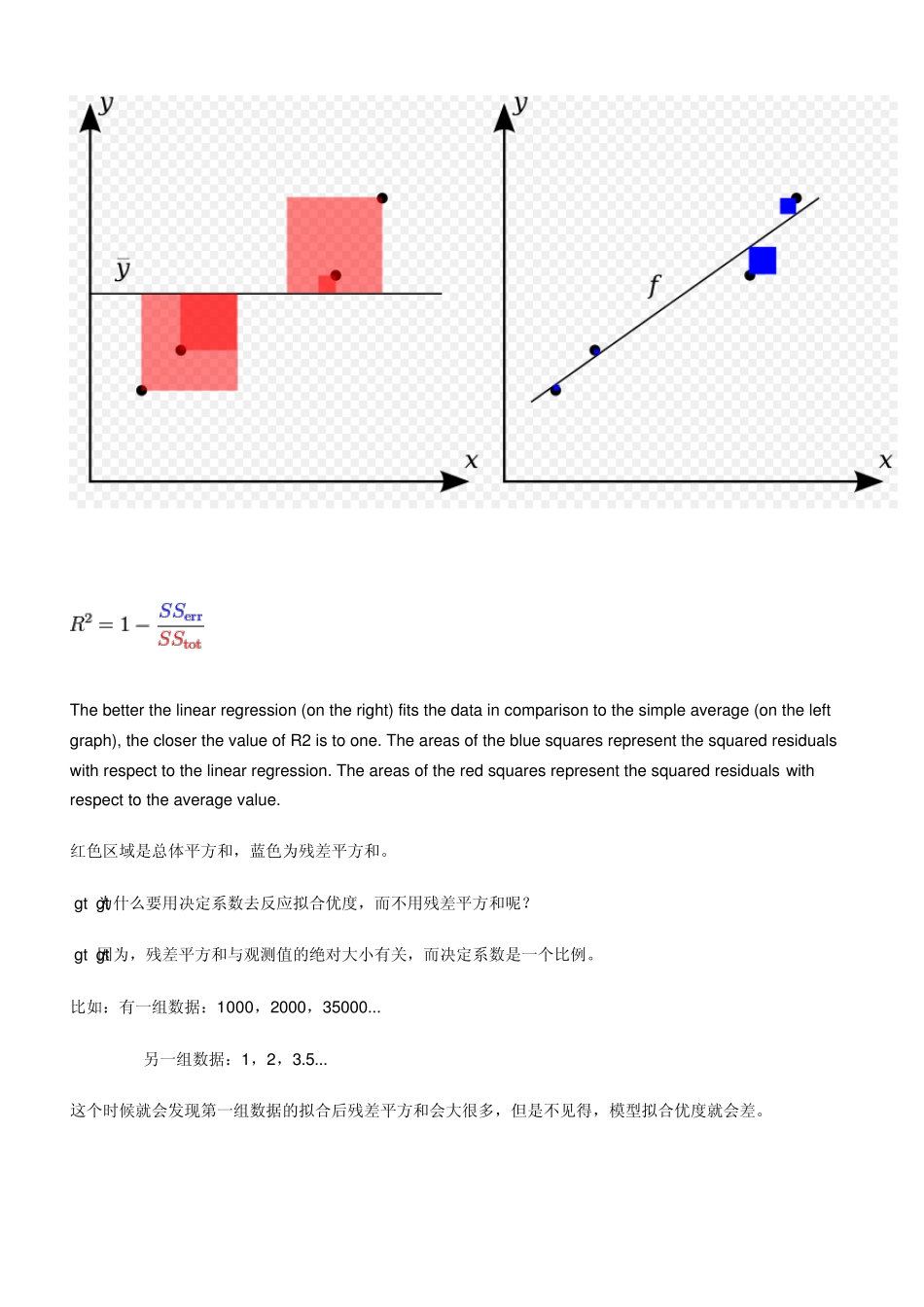
残差平方和 决定系数 首先看看几个定义: 总体平方和TSS( total su m of squ ares) 回归平方和RSS(regression su m of squ ares) 残差平方和ESS(Residu al su m of squ ares) 其中,y i表示实验数据,fi 表示模拟值,表示样本平均值。 决定系数(Coefficient of determination) 在一定程度上反应了模型的拟合优度。 其实就是回归平方和在总体平方和中所占的比例。因为 TSS=RSS+ESS The better the linear regression (on the right) fits the data in comparison to the simple average (on the left graph), the closer the value of R2 is to one. The areas of the blue squares represent the squared residuals w ith respect to the linear regression. The areas of the red squares represent the squared residuals w ith respect to the average value. 红色区域是总体平方和,蓝色为残差平方和。 >> 为什么要用决定系数去反应拟合优度,而不用残差平方和呢? >> 因为,残差平方和与观测值的绝对大小有关,而决定系数是一个比例。 比如:有一组数据:1000,2000,35000... 另一组数据:1,2,3.5... 这个时候就会发现第一组数据的拟合后残差平方和会大很多,但是不见得,模型拟合优度就会差。 第三章 一元线性回归 第一部分 学习指导 一、本章学习目的与要求 1、掌握一元线性回归的经典假设; 2、掌握一元线性回归的最小二乘法参数估计的计算公式、性质和应用; 3、理解拟合优度指标:决定系数 R2 的含义和作用; 4、掌握解释变量 X 和被解释变量Y 之间线性关系检验,回归参数0 和1 的显著性检验 5、了解利用回归方程进行预测的方法。 二、本章内容提要 (一)一元线性回归模型的假设条件 (1)E(i )=0 (i=1,2,„„,n),即随机误差项分布的均值为零。 (2)Var(i )=2 (i=1,2, „„,n),即随机误差项方差恒定,称为同方差。 ( 3 ) C o v (i ,j) = 0 ,( 任 意 i ≠ j , i , j = 1 , 2 , „ „ , n ), 即 随 机 误 差 项 之 间 互 不 相关。 (4)解释变量 X 是非随机的,换句话说,在重复抽样下, X 的取值是确定不变的。 (5)i ~N(0,2 ),即随机误差项服从均值为 0,方差为2 的正态分布。 前...