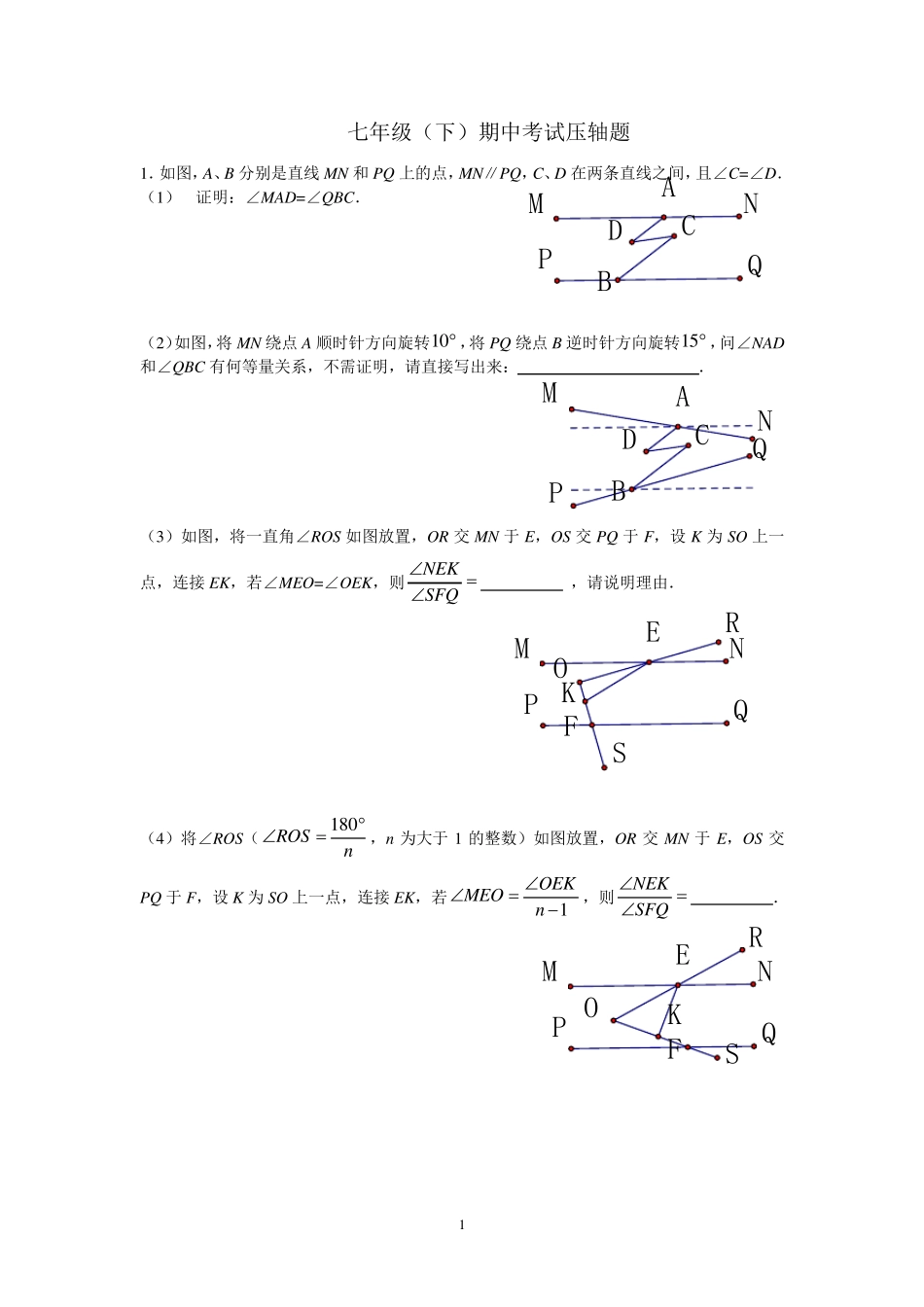
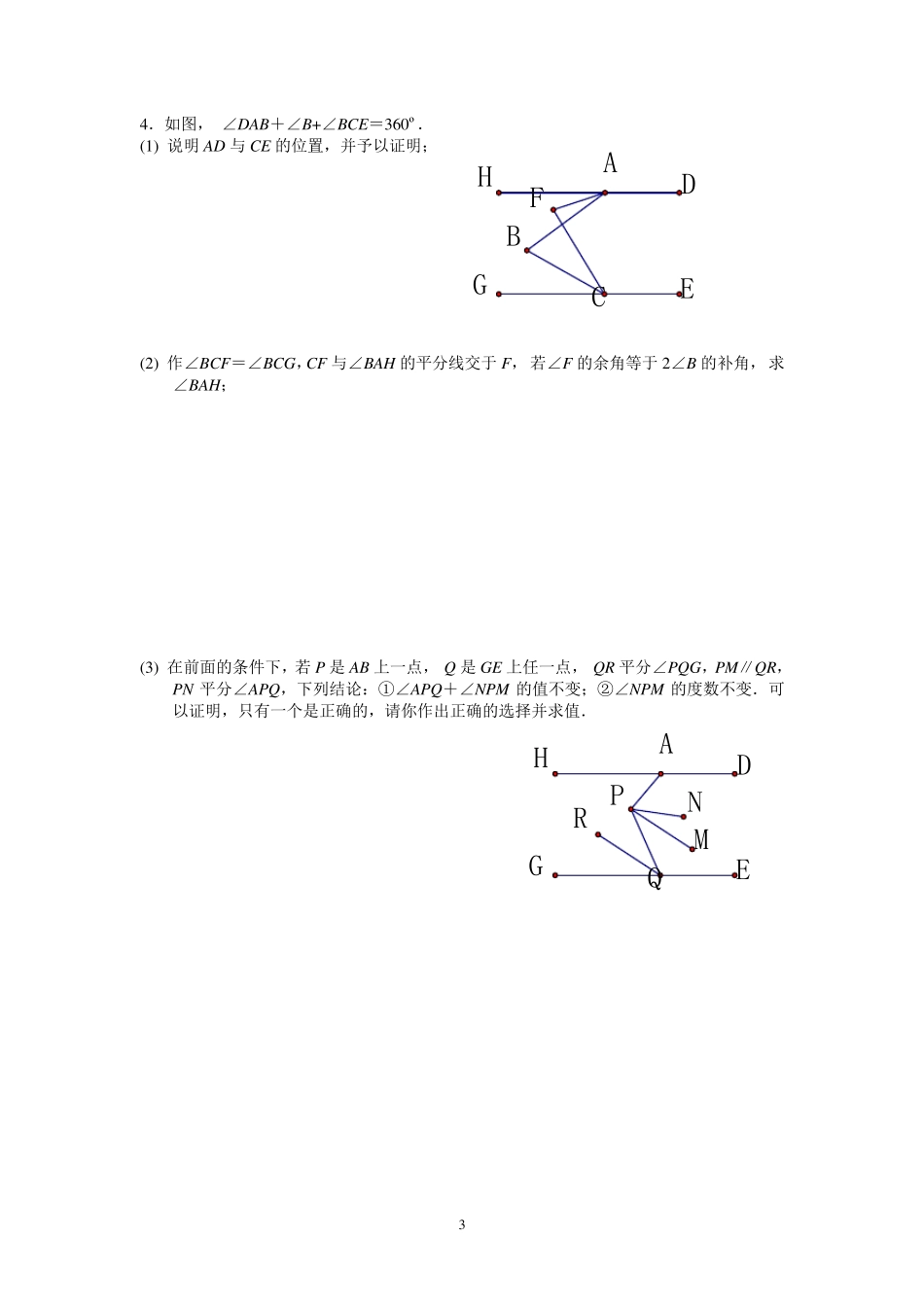
1 QPNMDABCQMNDPABCKSFRQNMOPESRQNMOPEFK七年级(下)期中考试压轴题 1.如图,A、B 分别是直线MN 和PQ 上的点,MN∥PQ,C、D 在两条直线之间,且∠C=∠D. (1) 证明:∠MAD=∠QBC. (2)如图,将 MN 绕点A 顺时针方向旋转10 ,将 PQ 绕点B 逆时针方向旋转15 ,问∠NAD和∠QBC 有何等量关系,不需证明,请直接写出来: . (3)如图,将一直角∠ROS 如图放置,OR 交 MN 于 E,OS 交 PQ 于 F,设 K 为 SO 上一点,连接 EK,若∠MEO=∠OEK,则NEKSFQ ,请说明理由. (4)将∠ROS(180ROSn,n 为大于 1 的整数)如图放置,OR 交 MN 于 E,OS 交PQ 于 F,设 K 为 SO 上一点,连接 EK,若1OEKMEOn,则NEKSFQ . 2 l1l2l3DCABPCGBHEDACGE HBDAFMN2 .如图,已知直线1l∥2l,点A、B 分别在1l、2l上,直线3l和直线1l、2l交于点C、D,直线CD 上有一点P; (1 )若点P 在点C、D 之间运动时,问∠PAC,∠APB,∠PBD 之间的关系是否发生变化.请说明理由; (2 )若点P 在点C、D 两点的外侧运动时(点P 与点C、D 不重合),试探索∠PAC,∠APB,∠PBD 之间的关系又是如何?请说明理由. 3 .如图,点E 在直线BH、DC 之间,点A 为 BH 上一点,且 AE⊥CE,9 0DCEHAE. (1 )求证:BH∥CD. (2 )如图:直线AF 交DC 于F,AM 平分∠EAF,AN 平分∠BAE.试探究∠ MAN ,∠AFG的数量关系. 3 FCEDHBGAQEPHDGANMR4.如图, ∠DAB+∠B+∠BCE=360º. (1) 说 明 AD 与 CE 的 位 置 ,并 予 以 证 明 ; (2) 作 ∠BCF=∠BCG,CF 与 ∠BAH 的 平 分 线 交 于 F, 若 ∠F 的 余 角 等 于 2∠B 的 补 角 , 求∠BAH; (3) 在 前 面 的 条 件 下 ,若 P 是 AB 上 一 点 , Q 是 GE 上 任 一 点 , QR平 分 ∠PQG,PM∥ QR,PN 平 分 ∠APQ,下 列 结 论 : ① ∠APQ+∠NPM 的 值 不 变 ; ② ∠NPM 的 度 数 不 变 .可以 证 明 ,只 有 一 个 是 正 确 的 ,请 你 作 出 正 确 的 选 择 并 求 值 . 4 xyQNMBAOxyPGFEBAOCD5 .如图,在平面直角坐标系中,A(m,n),点B(-1 ,n),且231 83210mnmn. (1 )求点A、B 的坐标; (2 )若点M(-3 ,0 ),在y 轴的负半轴上是...