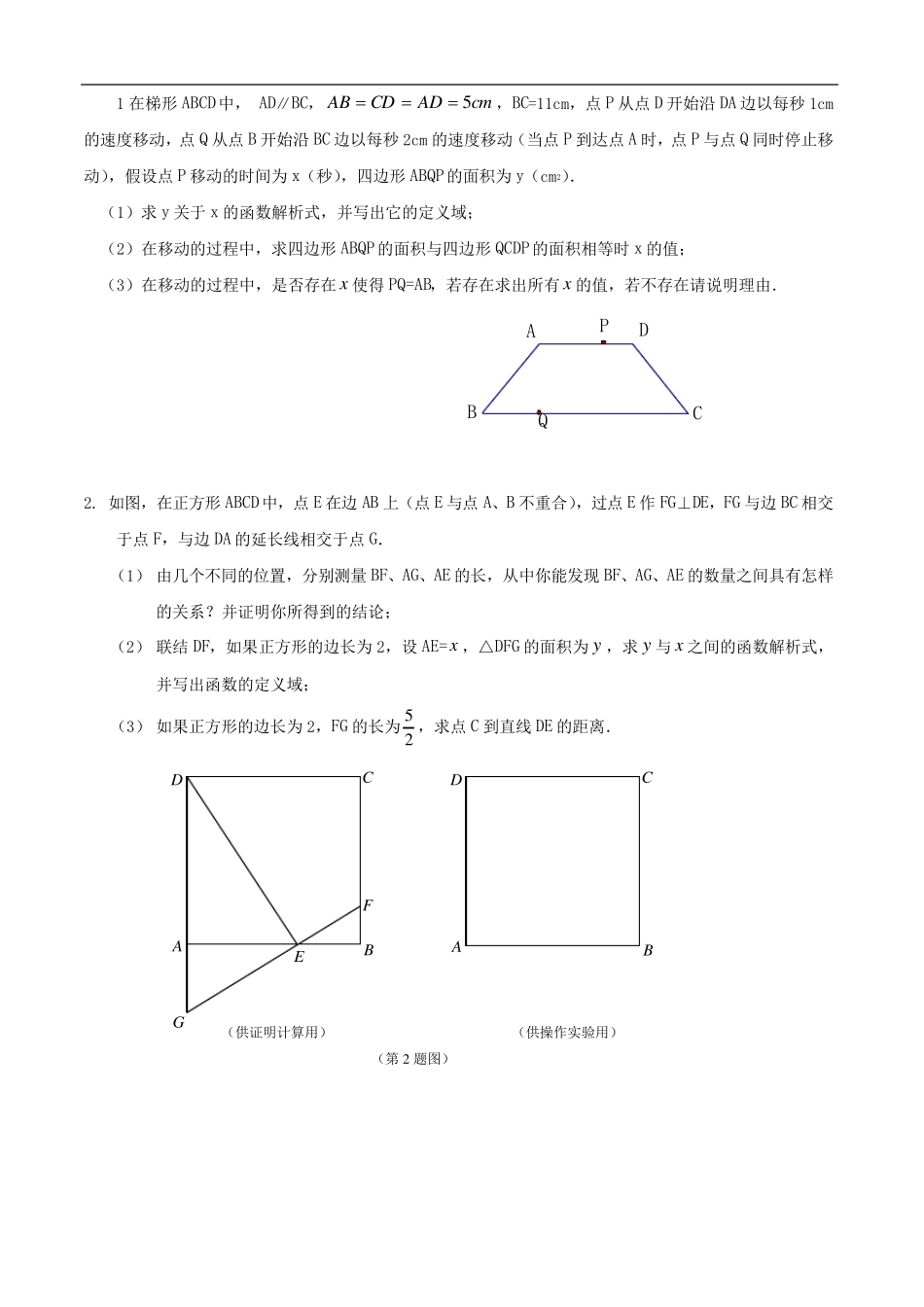
1 在梯形ABCD中, AD∥BC,cmADCDAB5,BC=11cm,点 P 从点 D 开始沿 DA 边以每秒 1cm的速度移动,点 Q 从点 B 开始沿 BC 边以每秒 2cm 的速度移动(当点 P 到达点 A 时,点 P 与点 Q 同时停止移动),假设点 P 移动的时间为 x(秒),四边形ABQP的面积为 y(cm2). (1)求 y 关于 x 的函数解析式,并写出它的定义域; (2)在移动的过程中,求四边形ABQP的面积与四边形QCDP的面积相等时 x 的值; (3)在移动的过程中,是否存在x使得 PQ=AB,若存在求出所有 x的值,若不存在请说明理由. 2. 如图,在正方形ABCD中,点 E 在边 AB 上(点 E 与点 A、B 不重合),过点 E 作 FG⊥DE,FG 与边 BC 相交于点 F,与边 DA 的延长线相交于点 G. (1) 由几个不同的位置,分别测量 BF、AG、AE 的长,从中你能发现 BF、AG、AE 的数量之间具有怎样的关系?并证明你所得到的结论; (2) 联结 DF,如果正方形的边长为 2,设 AE=x,△DFG 的面积为 y,求 y与 x之间的函数解析式,并写出函数的定义域; (3) 如果正方形的边长为 2,FG 的长为 25 ,求点 C 到直线 DE 的距离. DCBAPQ (供操作实验用) (供证明计算用) (第 2 题图) D A C B G F E D A C B 3.如图,已知在矩形ABCD中,对角线AC、BD 交于点O,CE=AE,F 是AE 的中点,AB = 4,BC = 8.求线段OF 的长. 4 已知一次函数421xy的图像与x 轴、y 轴分别相交于点A、B.梯形AOBC的边AC = 5. (1)求点C 的坐标; 为常数,且(2)如果点A、C 在一次函数yk xb(k、bk<0)的图像上,求这个一次函数的解析式. 5.如图,直角坐标平面xoy 中,点A 在x 轴上,点C 与点E 在y 轴上, 且E 为OC 中点,BC//x 轴,且BE⊥AE,联结AB, (1)求证:AE 平分∠BAO; (2)当 OE=6, BC=4 时,求直线AB 的解析式. 6.如图,△ABC 中,点D、E 分别是边BC、AC 的中点,过点A 作 AF//BC交线段DE 的延长线相交于F 点,取 AF 的中点G,如果BC = 2 AB. 求证:(1)四边形ABDF是菱形; (2)AC = 2DG. A B C D O E F (第 3 题图) y O x (第 4 题图) A B A B C O 第 5 题图 x y 。 E A B F D E G 第 6 题图 7.边长为4 的正方形ABCD中,点O 是对角线AC 的中点, P 是对角线AC 上一动点...