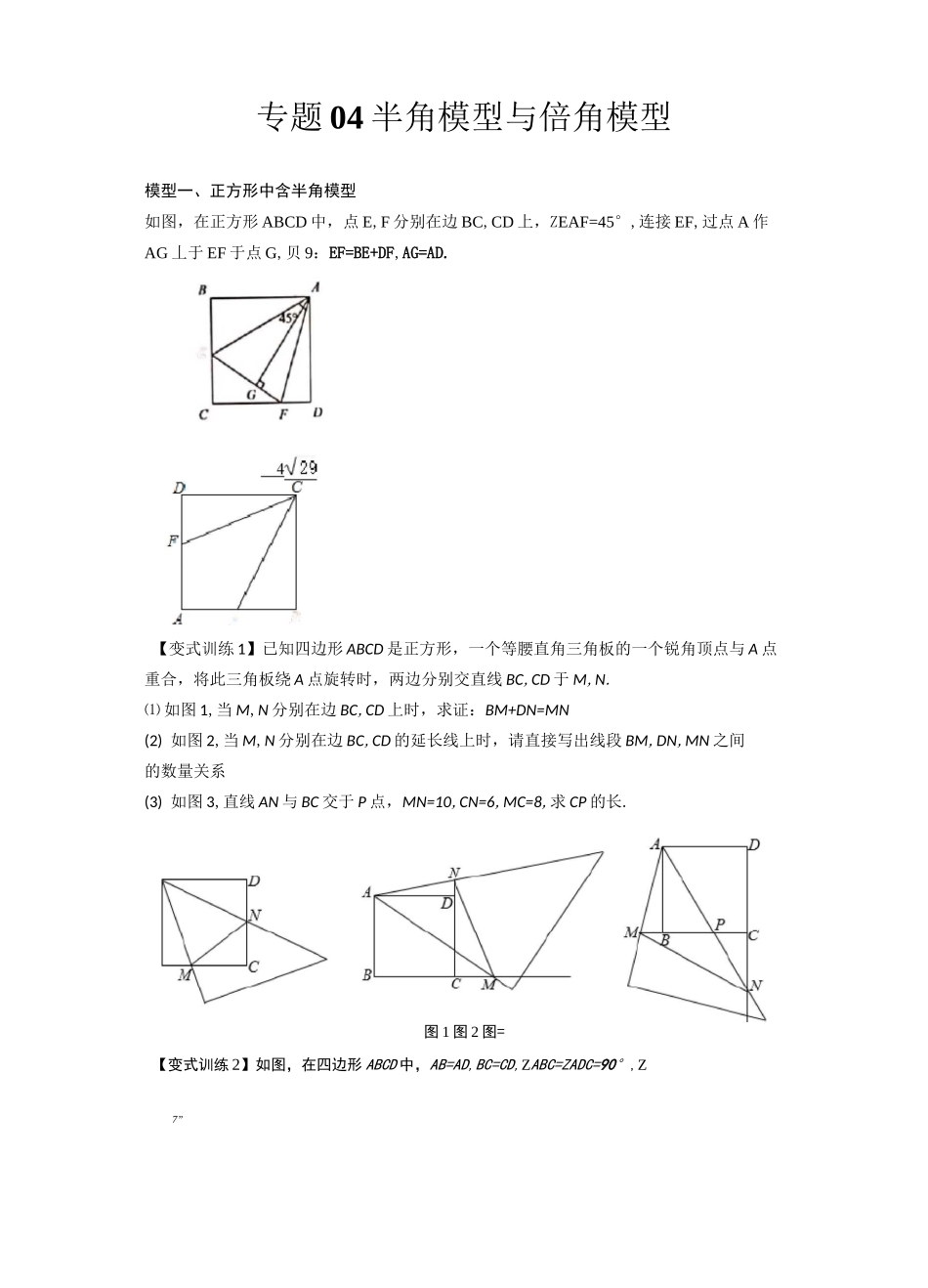
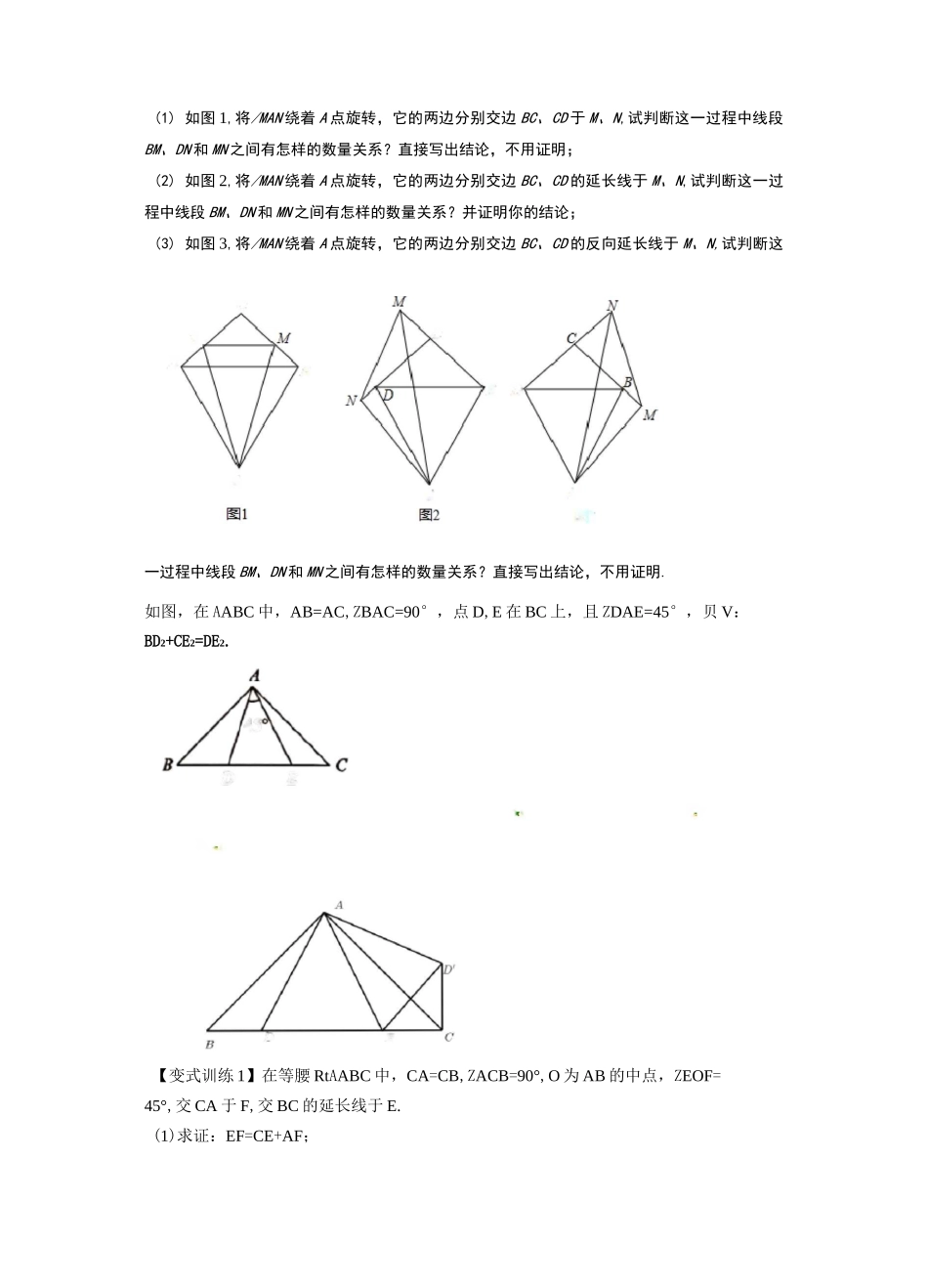
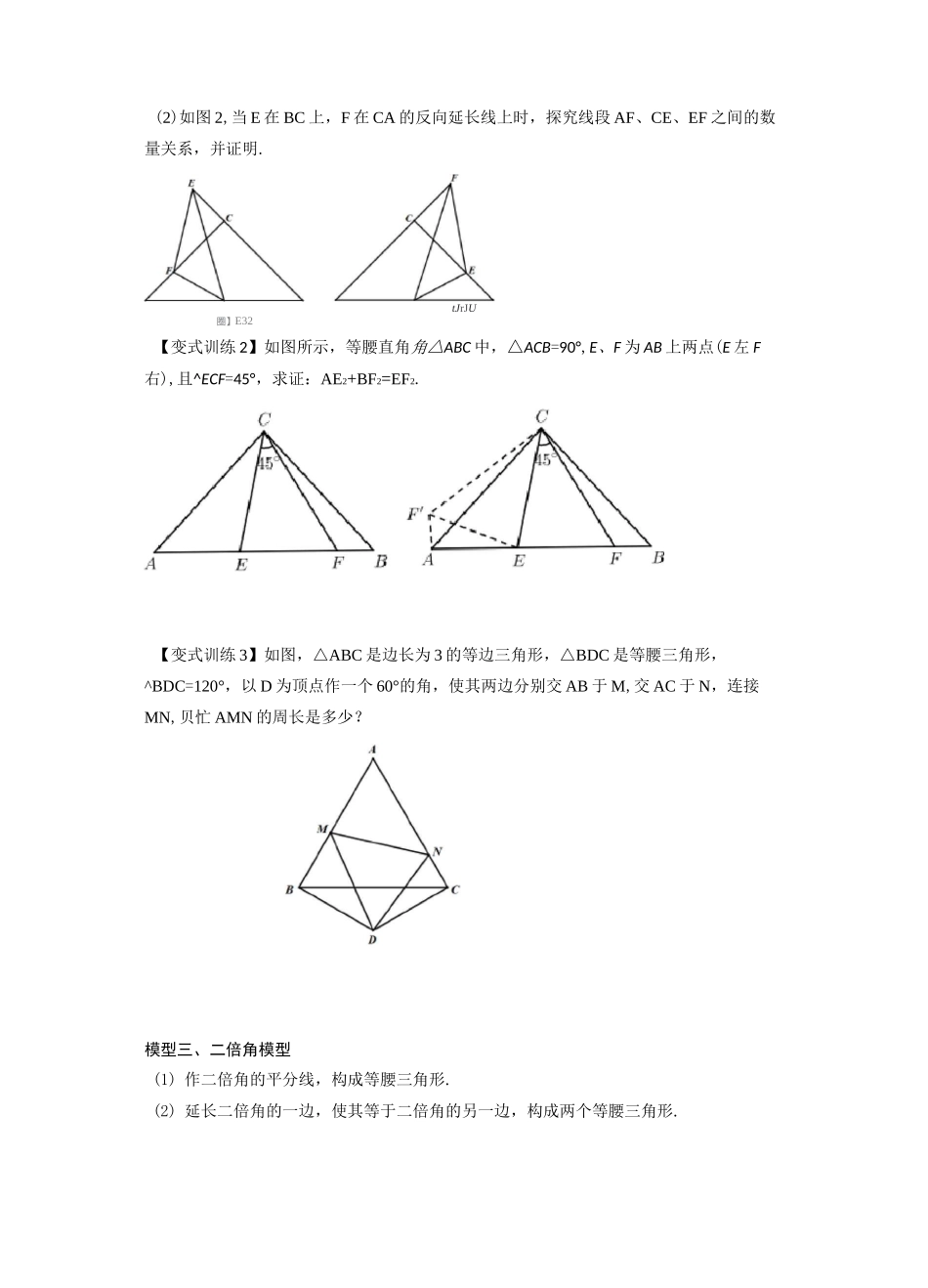
7”EBE例•如图,正方形/EC?的边长为 4,点 E,F 分别在 AB,AD 上,若 CE=5,且 ZECF=45°,则 CF 的长为_•专题 04 半角模型与倍角模型模型一、正方形中含半角模型如图,在正方形 ABCD 中,点 E,F 分别在边 BC,CD 上,ZEAF=45°,连接 EF,过点 A 作AG 丄于 EF 于点 G,贝 9:EF=BE+DF,AG=AD.【变式训练 1】已知四边形 ABCD 是正方形,一个等腰直角三角板的一个锐角顶点与 A 点重合,将此三角板绕 A 点旋转时,两边分别交直线 BC,CD 于 M,N.⑴ 如图 1,当 M,N 分别在边 BC,CD 上时,求证:BM+DN=MN(2) 如图 2,当 M,N 分别在边 BC,CD 的延长线上时,请直接写出线段 BM,DN,MN 之间的数量关系(3) 如图 3,直线 AN 与 BC 交于 P 点,MN=10,CN=6,MC=8,求 CP 的长.图 1 图 2 图=【变式训练 2】如图,在四边形 ABCD 中,AB=AD,BC=CD,ZABC=ZADC=90°,Z4DEDE例•如图,已知 DABC 中,□BAC=90。,AB=AC,D,E 是 BC 边上的点,将 DABD 绕点 A得至忙 ACD',当口 DAE=45。时,求证:DE=D,E;在(1)的条件下,猜想:BD2,DE2,CE2有怎样的数量关系?请写出,并说明理CCNDSSDAAA图模型二、等腰直角三角形角含半角模型(1) 如图 1,将/MAN 绕着 A 点旋转,它的两边分别交边 BC、CD 于 M、N,试判断这一过程中线段BM、DN 和 MN 之间有怎样的数量关系?直接写出结论,不用证明;(2) 如图 2,将/MAN 绕着 A 点旋转,它的两边分别交边 BC、CD 的延长线于 M、N,试判断这一过程中线段 BM、DN 和 MN 之间有怎样的数量关系?并证明你的结论;(3) 如图 3,将/MAN 绕着 A 点旋转,它的两边分别交边 BC、CD 的反向延长线于 M、N,试判断这一过程中线段 BM、DN 和 MN 之间有怎样的数量关系?直接写出结论,不用证明.如图,在 AABC 中,AB=AC,ZBAC=90°,点 D,E 在 BC 上,且 ZDAE=45°,贝 V:BD2+CE2=DE2.【变式训练 1】在等腰 RtAABC 中,CA=CB,ZACB=90°,O 为 AB 的中点,ZEOF=45°,交 CA 于 F,交 BC 的延长线于 E.(1)求证:EF=CE+AF;(2)如图 2,当 E 在 BC 上,F 在 CA 的反向延长线上时,探究线段 AF、CE、EF 之间的数量关系,并证明.tJrJU圈】E32【变式训练 2】如图所示,等腰直角角△ABC 中,△ACB=90°,E、F 为 AB 上两点(E 左 F右),且^ECF=45°,求证:AE2+BF2=EF2.【变式训练 3】如图,△ABC 是边长为 3 的等边三角形,△...