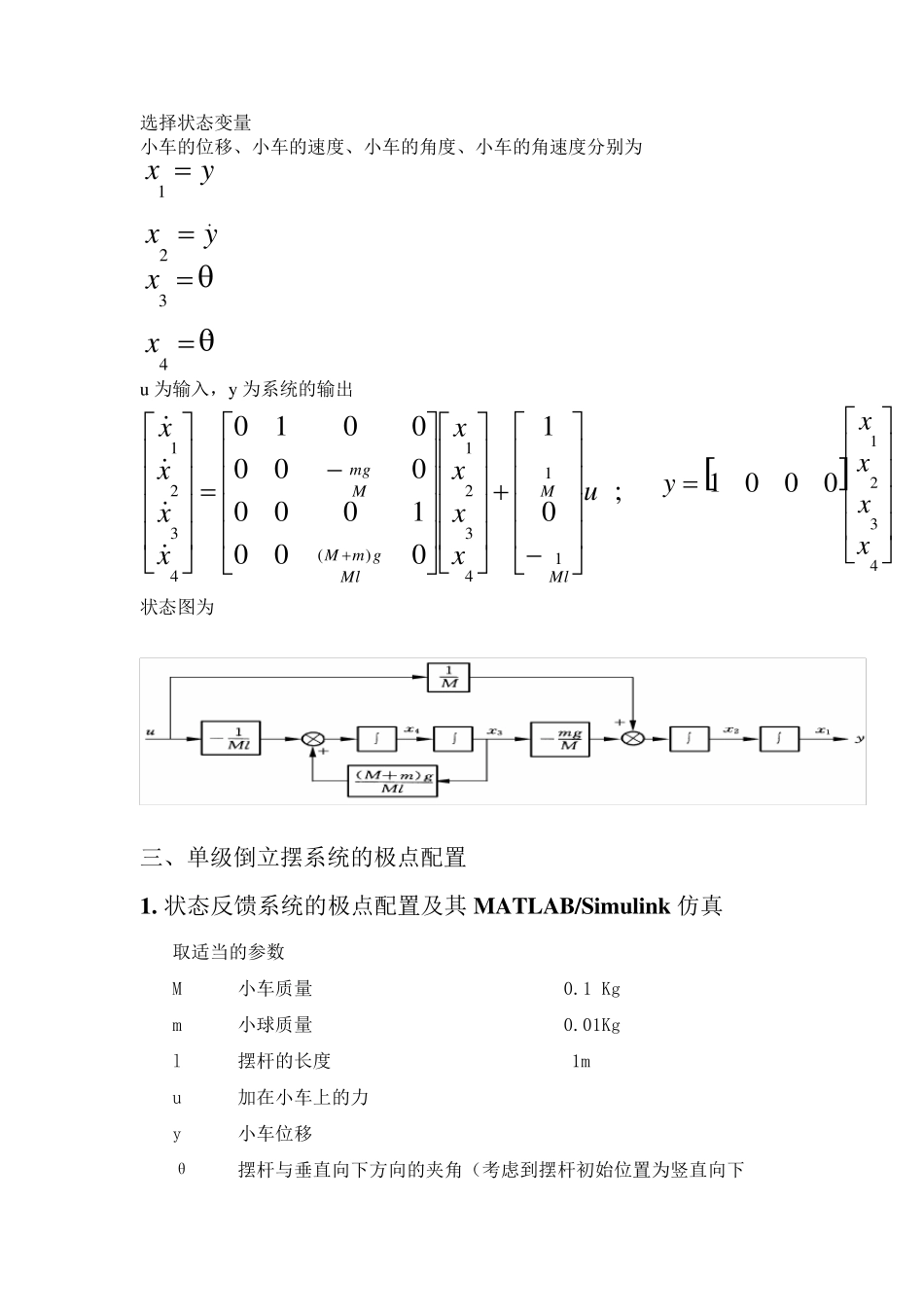
倒立摆在matlab 的simu link 库下的仿真 倒立摆是处于倒置不稳定状态,人为控制使其处于动态平衡的一种摆。对于倒立摆系统的控制研究长期以来被认为是控制理论及其应用领域里引起人们极大兴趣的问题,倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统。研究倒立摆控制能有效地反映控制中的许多问题,倒立摆研究具有重要的理论价值和应用价值,理论上,它是检验各种新的控制理论和方法的有效实验装置。应用上,倒立摆广泛应用于控制理论研究!航空航天控制,机器人、杂技顶杆表演等领域,在自动化领域中具有重要的价值。另外,由于此装置成本低廉,结构简单,便于用模拟、数字等不同方式控制,在控制理论教学和科研中也有很多应用。 本论文中,以一级倒立摆为研究对象,对它的起摆以及稳定控制做了研究,主要研究工作如下: 1.首先介绍了倒立摆系统的组成和控制原理,建立了一级倒立摆的数学模型,对倒立摆系统进行定性分析,但在平衡点是能控的、能观的。 2.分析了倒立摆的起摆过程,对倒立摆的起摆能量反馈控制进行分析与说明。 3.在matlab2014a 的simu link 库下对倒立摆构造单级倒立摆状态反馈控制系统的仿真模型和构造具有状态观测器的单级倒立摆状态反馈控制系统的仿真模型。 4.对这次仿真的总结。 一、倒立摆的控制目标 倒立摆的控制问题就是使摆杆尽快地达到一个平衡位置,并且使之没有大的振荡和过大的角度和速度。当摆杆到达期望的位置后,系统能克服随机扰动而保持稳定的位置。 二、建立单级倒立摆系统的状态空间模型 其中,质量为M 的小车在水平方向滑动,质量为m 的球连在长度为L 的刚性摆一端,x 表示小车的位移,u 是作用在小车上的力,通过移动小车使带有小球的摆杆始终处于垂直的位置。为了简单起见,假设小车和摆仅在一个平面内运动,且不考虑摩擦、摆杆的质量和空气阻力。如图 1 图 1 设系统的动态特性可以用小车的位移和速度及杆偏离垂线的角度θ 和角速度 来描述。设小车位移为 x,则小球中心位置是lsinx 在水平方向,应用牛顿第二定律: 2222d xd(xsin)ddMmlutt 在垂直于摆杆方向,应用牛顿第二定律: 22d(xsin)sindmlmgt 求微分方程得: )(cos)(sinddt cos)sin()(sindd222t )sin()(cosddt )sin()cos()(cosdd222t 线性化:当和较小时 ,有• 和 较小时 ,有 01coss...