第2 章 信号分析 本章提要 信号分类 周期信号分析--傅里叶级数 非周期信号分析--傅里叶变换 脉冲函数及其性质 信号:反映研究对象状态和运动特征的物理量 信号分析:从信号中提取有用信息的方法和手段 §2 -1 信号的分类 两大类:确定性信号,非确定性信号 确定性信号:给定条件下取值是确定的。 进一步分为:周期信号,非周期信号。 质量M 弹簧 刚度K t x (t) o x 0 质量-弹簧系统的力学模型 x (t) 0cos)(tmkAtx 非确定性信号(随机信号):给定条件下取值是不确定的 按取值情况分类:模拟信号,离散信号 数字信号:属于离散信号,幅值离散,并用二进制表示。 信号描述方法 时域描述 如简谐信号 )cos(000tx 简谐信号及其三个要素 幅值 频率 相角 频域描述 以信号的频率结构来描述信号的方法:将信号看成许多谐波(简谐信号)之和,每一个谐波称作该信号的一个频率成分,考察信号含有那些频率的谐波,以及各谐波的幅值和相角。
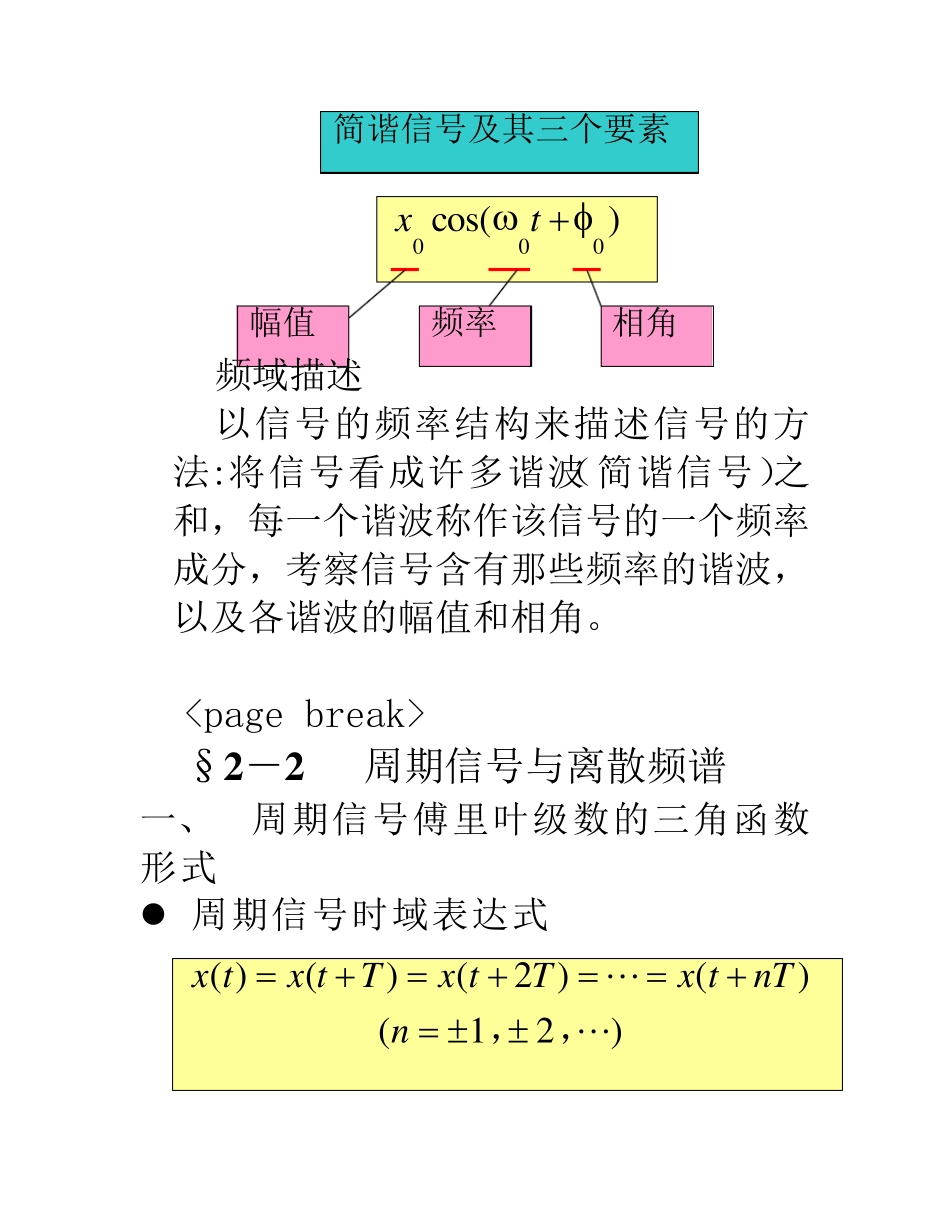
§2 -2 周期信号与离散频谱 一、 周期信号傅里叶级数的三角函数形式 周期信号时域表达式 )21()()2()()(,,nnTtxTtxTtxtx T:周期。注意n的取值:周期信号“无始无终” # 傅里叶级数的三角函数展开式 )sincos()(0100tnbtnaatxnnn (n=1, 2, 3,…) 傅立叶系数: 220)(1TTdttxTa 220cos)(2TTntdtntxTa 220sin)(2TTntdtntxTb 式中 T--周期;0--基频, 0=2/T。 三角函数展开式的另一种形式: )cos()(100 nnntnAatxN 次谐波 N 次谐波的相角 N 次谐波的频率 N 次谐波的幅值 信号的均值,直流分量 ,3,2,1arctg22nabbaAnnnnnn 周期信号可以看作均值与一系列谐波之和--谐波分析法 频谱图 ﹡﹡﹡ ﹡﹡﹡ nAn0 2 0 2 周期信号的频谱三个特点:离散性、谐波性、收敛性 例1:求周期性非对称周期方波的傅立叶级数并画出频谱图 解: t x (t) -A A T … … 非对称周期方波 周期方波 解: 信号的基频 T20 傅里叶系数 奇函数:00naa 为偶数为奇数nnnAnnAttnATttntxTbTTTn04cos12dsin4dsin)(2200220 t 的偶函...