半导体物理学(刘恩科)第七版第一章到第五章完整课后题答案

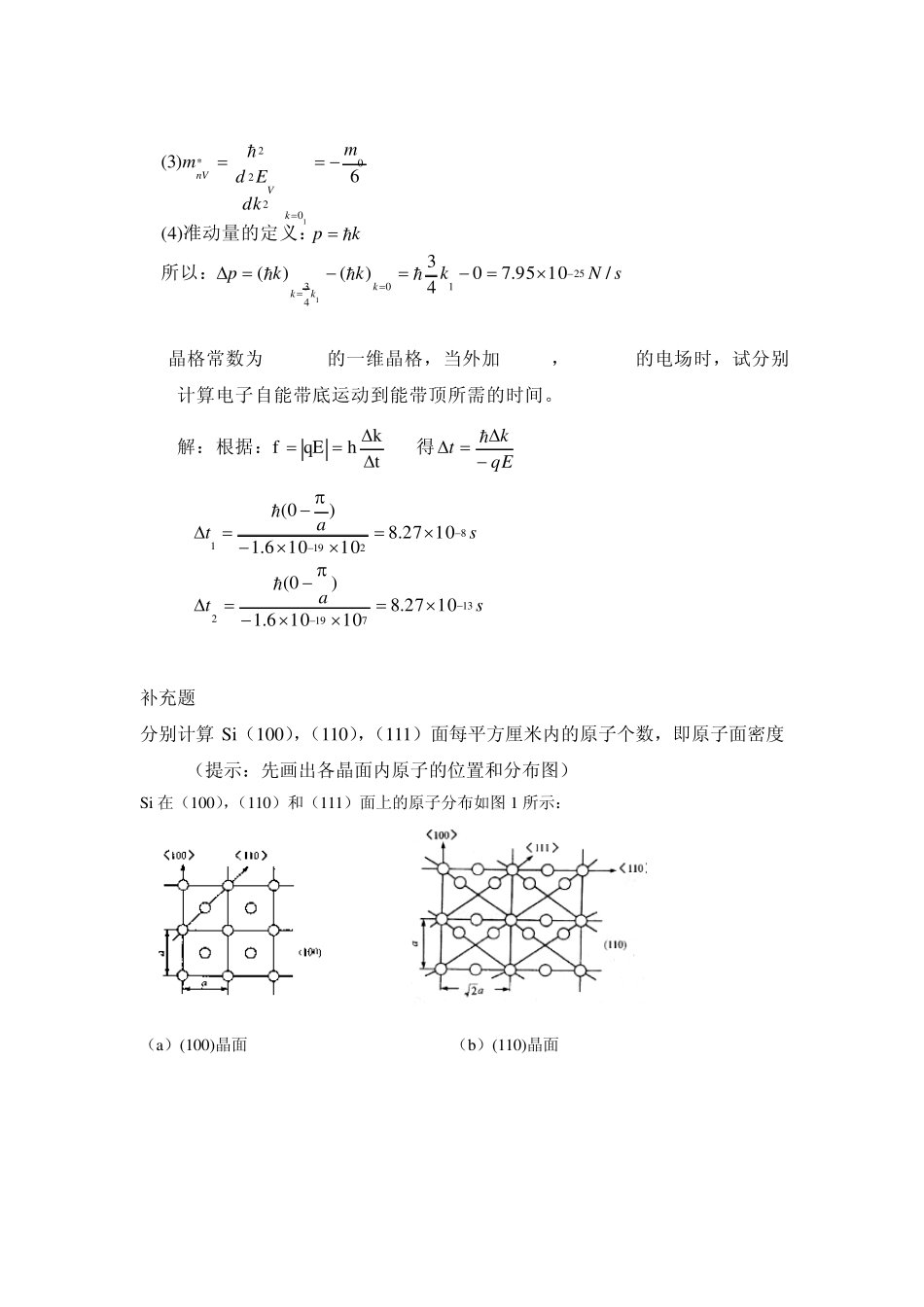
第一章习题 1．设晶格常数为a的一维晶格，导带极小值附近能量Ec(k)和价带极大值附近能量EV(k)分别为： Ec=0220122021202236)(,)(3mkhmkhkEmkkhmkhV 0m。试求：为电子惯性质量，nmaak3 1 4.0,1  （1）禁带宽度; （2）导带底电子有效质量; （3）价带顶电子有效质量; （4）价带顶电子跃迁到导带底时准动量的变化 解：（1） eVmkEkEEEkmdkEdkmkdkdEEckkmmmdkEdkkmkkmkVCgVVVc6 4.01 2)0()43(0,0600643038232430)(2320212102220202020222101202因此：取极大值处，所以又因为得价带：取极小值处，所以：在又因为：得：由导带： 043222*83)2(1mdkEdmkkCnC sNkkkpkpmdkEdmkkkkVnV/1095.7043)()()4(6)3(25104300222*11所以：准动量的定义： 2. 晶格常数为0.25nm的一维晶格，当外加102V/m，107 V/m的电场时，试分别计算电子自能带底运动到能带顶所需的时间。 解：根据：tkhqEf 得qEkt satsat137192821911027.810106.1)0(1027.810106.1)0( 补充题 1 分别计算Si（100），（110），（111）面每平方厘米内的原子个数，即原子面密度（提示：先画出各晶面内原子的位置和分布图） Si 在（100），（110）和（111）面上的原子分布如图 1 所示： （a）(100)晶面 （b）(110)晶面 （c）(111)晶面 补充题2 一维晶体的电子能带可写为)2cos81cos87()22kakamakE （， 式中a 为 晶格常数，试求 （1）布里渊区边界； （2）能带宽度； （3）电子在波矢k 状态时的速度； （4）能带底部电子的有效质量*nm ； （5）能带顶部空穴的有效质量*pm 解：（1）由0)(dkkdE 得 ank （n=0，1，2…） 进一步分析ank)12( ，E（k）有极大值， 214221422142822/1083.7342232212414111/1059.92422124142110/1078.6)1043.5(224141100cmatomaaacmatomaaacmatomaa）：（）：（）：（ 222)makEMAX（ ank2时，E（k）有极小值 所以布里渊区边界为ank)12( (2)能带宽度为222)()makEkEMINMAX（ (3）电子在波矢k状态的速度)2sin41(sin1kakamadkdEv （4）电子的有效质量 )2cos21(cos222*kakamdkEdmn  能带底部 ank2 所以...