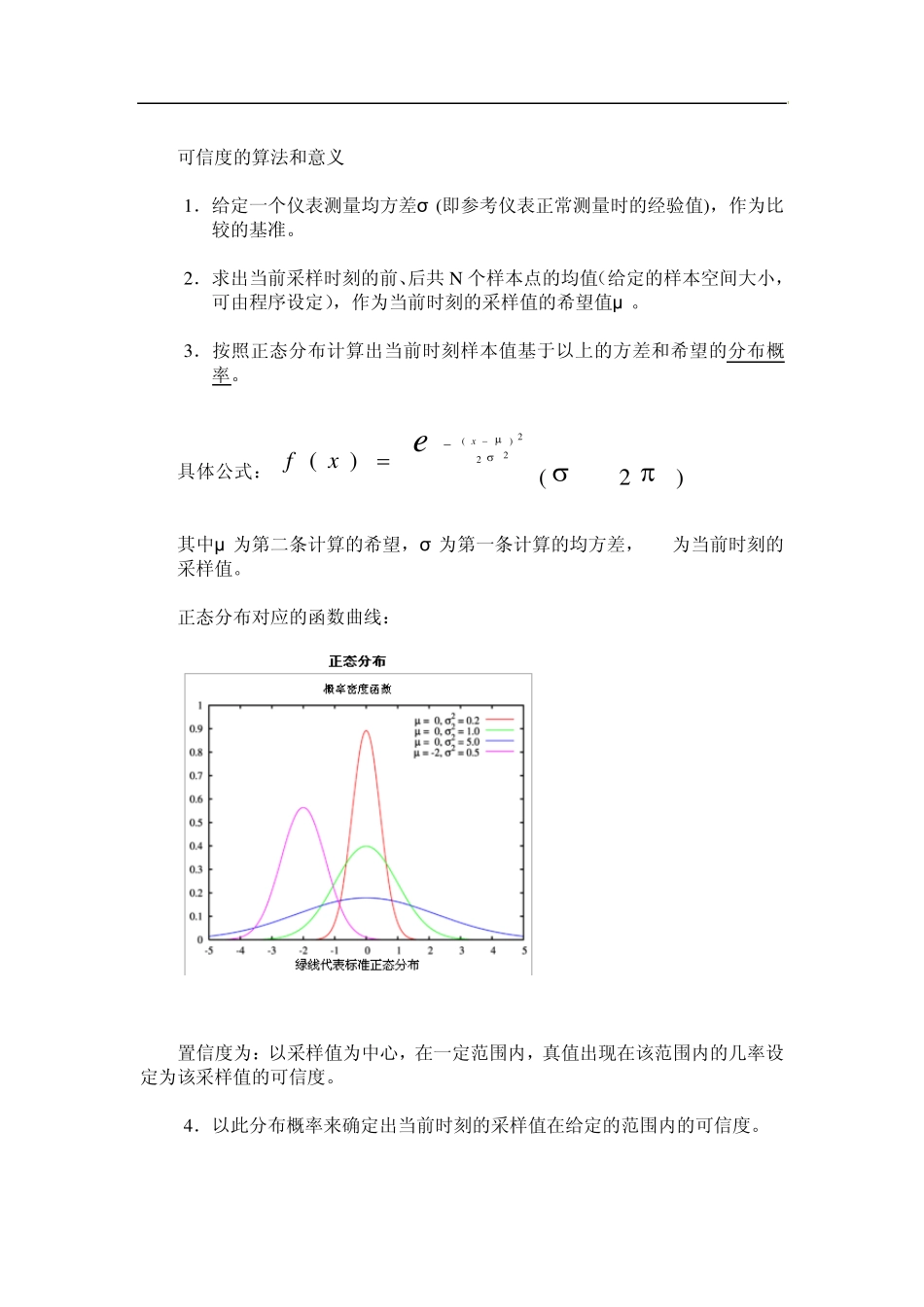
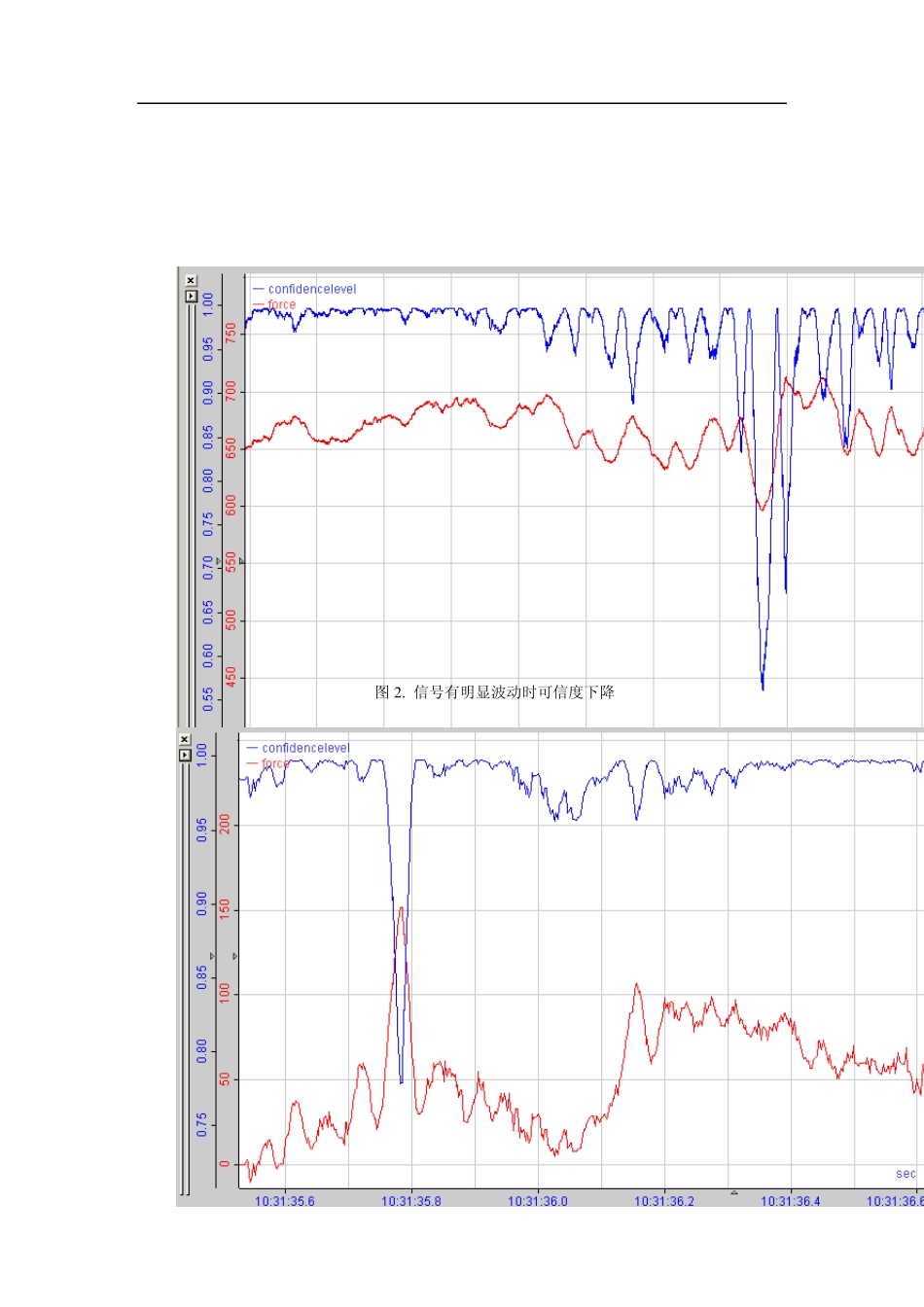
可信度的算法和意义 1.给定一个仪表测量均方差σ (即参考仪表正常测量时的经验值),作为比较的基准。 2.求出当前采样时刻的前、后共 N 个样本点的均值(给定的样本空间大小,可由程序设定),作为当前时刻的采样值的希望值μ 。 3.按照正态分布计算出当前时刻样本值基于以上的方差和希望的分布概率。 具体公式:)2()(222)(exxf 其中μ 为第二条计算的希望,σ 为第一条计算的均方差, x 为当前时刻的采样值。 正态分布对应的函数曲线: 置信度为:以采样值为中心,在一定范围内,真值出现在该范围内的几率设定为该采样值的可信度。 4.以此分布概率来确定出当前时刻的采样值在给定的范围内的可信度。 5.求出当前时刻所取到样本片段的均方差,根据不同的曲线设定最小不可信值,例如:认为均方差小于某个值时是完全不可信的,就判断该当前采样点的可信度为0。 6.按此算法滑动地算出曲线上每一个采样点的可信度,最后计算出所有采样点的可信度的平均值,得到整条曲线的整体可信度。此值存入二级数据库。 求单个采样值的可信度表达式如下: Express = ConfidenceLevel([0:0],N,0.2,σ ) 其中[0:0]:表示要分析的通道; N:给定的样本空间大小; 0.2: 表示最小不可信的均方差,即当计算出当前样本空间的均方差小于此值时,认为是不可信的。(例如:当遇到通信错误,曲线采集到的数据不发生变化时,认为是不可信的) 以下是分别对不同曲线的可信度分析的结果: 图 1. 有异常值时的实时可信度分析结果 由图 1 可以看出当采集的信号有明显的异常值时,该采样值算出来的可信度几乎为0,而在波动较大时,可信度也随之降低。 图2 . 信号有明显波动时可信度下降 图3 .信号有明显波动时可信度下降 以下是相同曲线设定不同样本空间时的可信度分析。 图4 . 样本空间设定为 3 0 0 0 , 某厚差曲线的可信度分析 图5 . 样本空间设定为 1 0 0 0 ,某厚差曲线的可信度分析 图6 . 样本空间设定为 5 0 0 ,某厚差曲线的可信度分析 图7 样本空间设定为300,某厚差曲线的可信度分析 因为涉及到概率统计,所以需要有一定量的样本空间,一般在300 点以上,但是样本空间太大,又影响实时性的分析,所以建议样本空间选择在300~1000点之间。