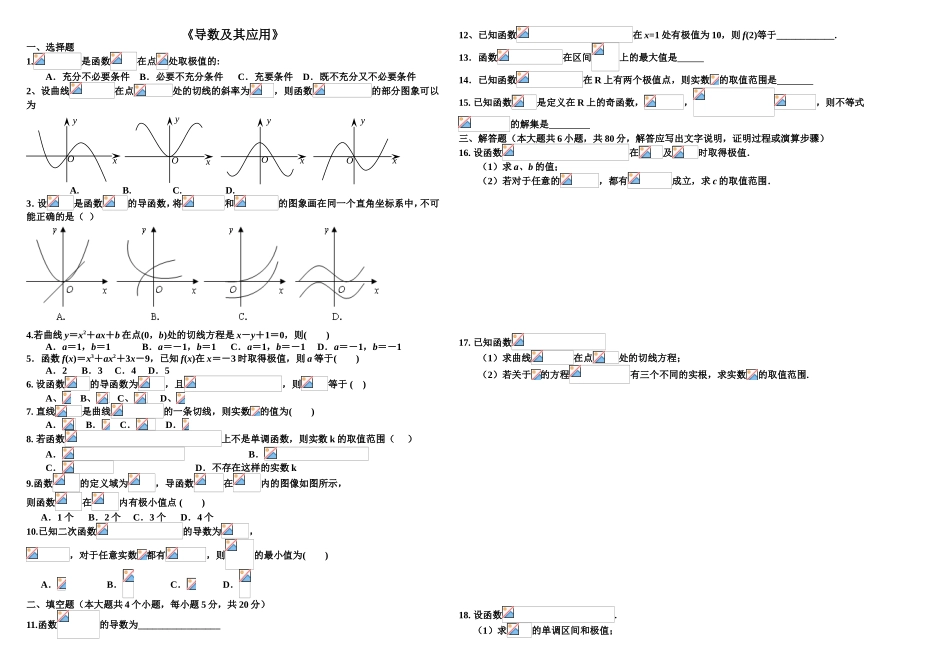
《导数及其应用》一、选择题1.是函数在点处取极值的:A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件2、设曲线在点处的切线的斜率为,则函数的部分图象可以为A.B.C.D.3.设是函数的导函数,将和的图象画在同一个直角坐标系中,不可能正确的是()4.若曲线y=x2+ax+b在点(0,b)处的切线方程是x-y+1=0,则()A.a=1,b=1B.a=-1,b=1C.a=1,b=-1D.a=-1,b=-15.函数f(x)=x3+ax2+3x-9,已知f(x)在x=-3时取得极值,则a等于()A.2B.3C.4D.56.设函数的导函数为,且,则等于()A、B、C、D、7.直线是曲线的一条切线,则实数的值为()A.B.C.D.8.若函数上不是单调函数,则实数k的取值范围()A.B.C.D.不存在这样的实数k9.函数的定义域为,导函数在内的图像如图所示,则函数在内有极小值点()A.1个B.2个C.3个D.4个10.已知二次函数的导数为,,对于任意实数都有,则的最小值为()A.B.C.D.二、填空题(本大题共4个小题,每小题5分,共20分)11.函数的导数为_________________12、已知函数在x=1处有极值为10,则f(2)等于____________.13.函数在区间上的最大值是14.已知函数在R上有两个极值点,则实数的取值范围是15.已知函数是定义在R上的奇函数,,,则不等式的解集是三、解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)16.设函数在及时取得极值.(1)求a、b的值;(2)若对于任意的,都有成立,求c的取值范围.17.已知函数(1)求曲线在点处的切线方程;(2)若关于的方程有三个不同的实根,求实数的取值范围.18.设函数.(1)求的单调区间和极值;OxxxxyyyyOOO(2)若关于的方程有3个不同实根,求实数的取值范围.(3)已知当恒成立,求实数的取值范围.19.(本题满分12分)已知函数.(Ⅰ)求的最小值;(Ⅱ)若对所有都有,求实数的取值范围.20.已知(1)当时,求函数的单调区间。(2)当时,讨论函数的单调增区间。(3)是否存在负实数,使,函数有最小值-3?21.已知函数,,其中.(1)若是函数的极值点,求实数的值;(2)若对任意的(为自然对数的底数)都有≥成立,求实数的取值范围.《导数及其应用》参考答案一、选择题:题号12345678910答案DADADBDBAC二、填空题:11.;12.1813.;14.;15.三、解答题16.解:(1),因为函数在及取得极值,则有,.即解得,.(2)由(Ⅰ)可知,,.当时,;当时,;当时,.所以,当时,取得极大值,又,.则当时,的最大值为.因为对于任意的,有恒成立,所以,解得或,因此的取值范围为..17.解(1)………………………2分∴曲线在处的切线方程为,即;……4分(2)记令或1.…………………………………………………………6分则的变化情况如下表极大极小当有极大值有极小值.………………………10分由的简图知,当且仅当即时,函数有三个不同零点,过点可作三条不同切线.所以若过点可作曲线的三条不同切线,的范围是.…………14分18.解:(1)…………………1分∴当,…………………2分∴的单调递增区间是,单调递减区间是……3分当;当.…………4分(2)由(1)可知图象的大致形状及走向(图略)∴当的图象有3个不同交点,……6分即当时方程有三解.…………………………………7分(3) 上恒成立.…………………………………………9分令,由二次函数的性质,上是增函数,∴∴所求的取值范围是……………………………………12分19.解析:的定义域为,…………1分的导数.………………3分令,解得;令,解得.从而在单调递减,在单调递增.………………5分所以,当时,取得最小值.…………………………6分(Ⅱ)解法一:令,则,……………………8分①若,当时,,故在上为增函数,所以,时,,即.……………………10分②若,方程的根为,此时,若,则,故在该区间为减函数.所以时,,即,与题设相矛盾.……………………13分综上,满足条件的的取值范围是.……………………………………14分解法二:依题意,得在上恒成立,即不等式对于恒成立.……………………8分令,则.……………………10分当时,因为,故是上的增函数,所以的最小值是,………………13分所...