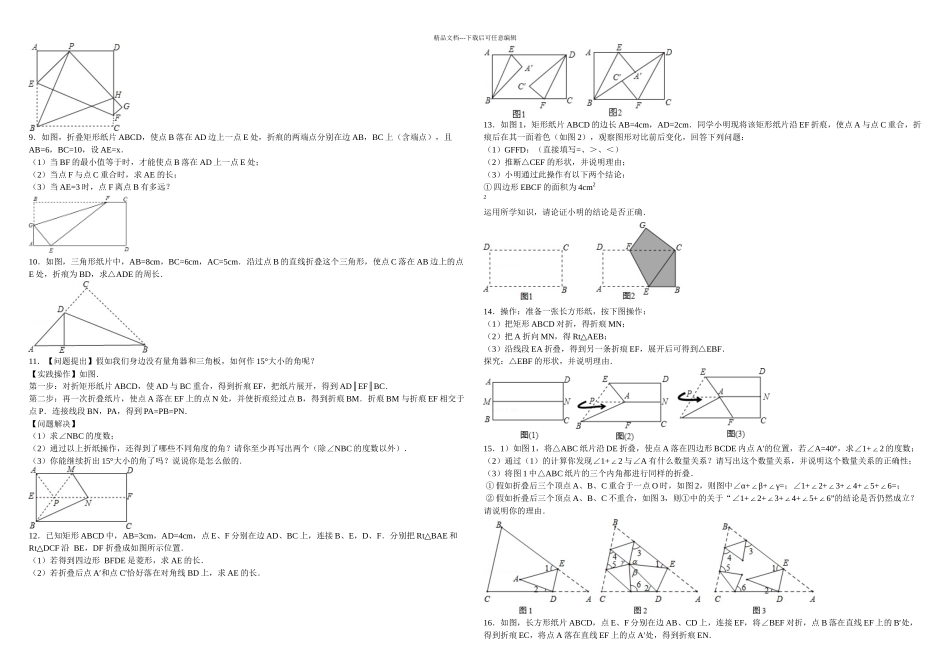
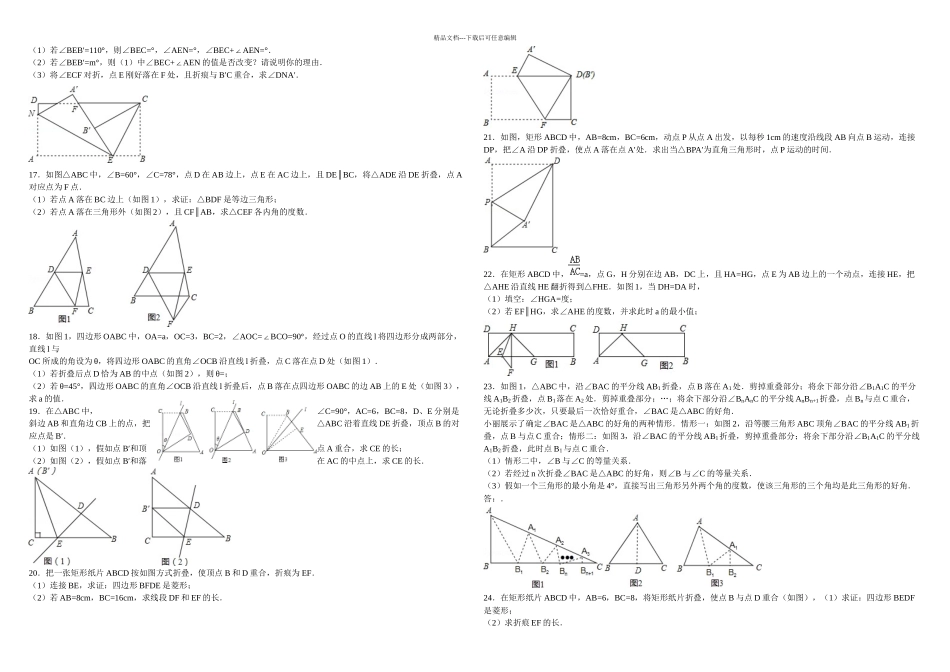
精品文档---下载后可任意编辑1.△AOB 在平面直角坐标系中的位置如图所示,其中,A(0,﹣3),B(﹣2,0),O 是坐标原点.(1)将△AOB 先作其关于 x 轴的对称图形,再把新图形向右平移 3 个单位,在图中画出两次变换后所得的图形△AO1B1;(2)若点 M(x,y)在△AOB 上,则它随上述两次变换后得到点 M1,则点 M1的坐标是.2.(1)数学课上,老师出了一道题,如图①,Rt ABC△中,∠C=90°,,求证:∠B=30°,请你完成证明过程.(2)如图②,四边形 ABCD 是一张边长为 2 的正方形纸片,E、F 分别为 AB、CD 的中点,沿过点 D 的折痕将纸片翻折,使点 A 落在 EF 上的点 A′处,折痕交 AE 于点 G,请运用(1)中的结论求∠ADG 的度数和 AG 的长.(3)若矩形纸片 ABCD 按如图③所示的方式折叠,B、D 两点恰好重合于一点 O(如图④),当 AB=6,求 EF 的长.3.如图,矩形 ABCD 中,AB=6,BC=8,点 E 是射线 CB 上的一个动点,把△DCE 沿 DE 折叠,点 C 的对应点为 C′.(1)若点 C′刚好落在对角线 BD 上时,BC′=; (2)若点 C′刚好落在线段 AB 的垂直平分线上时,求 CE 的长;(3)若点 C′刚好落在线段 AD 的垂直平分线上时,求 CE 的长.4.如图,矩形纸片 ABCD,将△AMP 和△BPQ 分别沿 PM 和 PQ 折叠(AP>AM),点 A 和点 B 都与点 E 重合;再将△CQD 沿 DQ 折叠,点 C 落在线段 EQ 上点 F 处.(1)推断△AMP,△BPQ,△CQD 和△FDM 中有哪几对相似三角形?(不需说明理由)(2)假如 AM=1,sinDMF=∠,求 AB 的长.5.如图,在矩形 ABCD 中,点 E 在边 CD 上,将该矩形沿 AE 折叠,使点 D 落在边 BC 上的点 F 处,过点 F 作分、FG CD∥,交 AE 于点 G 连接 DG.(1)求证:四边形 DEFG 为菱形;(2)若 CD=8,CF=4,求的值.6.如图 1,一张菱形纸片 EHGF,点 A、D、C、B 分别是 EF、EH、HG、GF 边上的点,连接AD、DC、CB、AB、DB,且 AD=,AB=;如图 2,若将△FAB、△AED、△DHC、△CGB 分别沿 AB、AD、DC、CB对折,点 E、F 都落在 DB 上的点 P 处,点 H、G 都落在 DB 上的点 Q 处.(1)求证:四边形 ADCB 是矩形;(2)求菱形纸片 EHGF 的面积和边长.7.(1)操作发现:如图①,在 Rt ABC△中,∠C=2B=90°∠,点 D 是 BC 上一点,沿 AD 折叠△ADC,使得点 C 恰好...