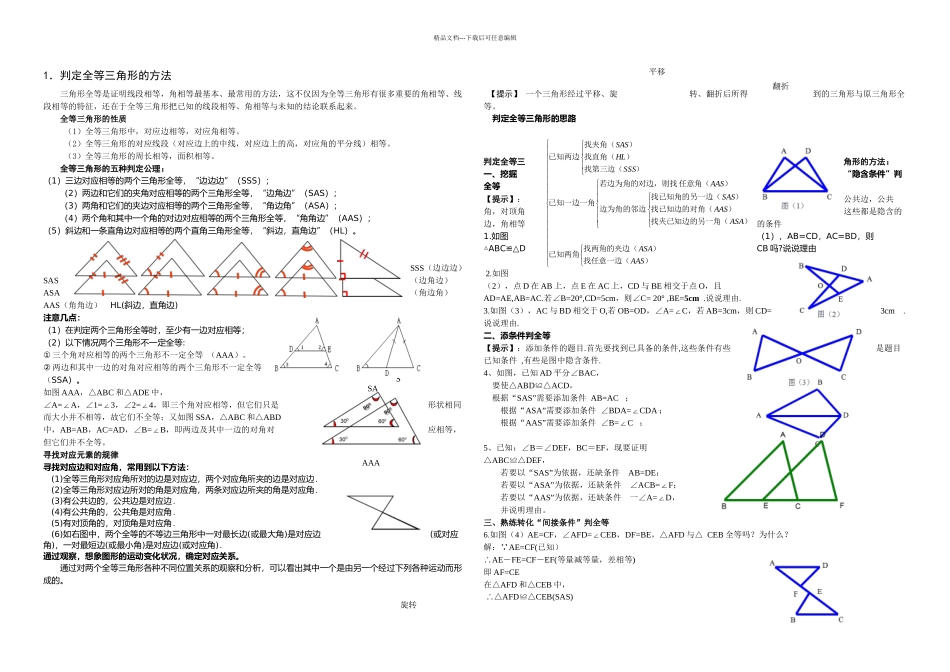
)找任意一边()找两角的夹边(已知两角)找夹已知边的另一角()找已知边的对角()找已知角的另一边(边为角的邻边)任意角(若边为角的对边,则找已知一边一角)找第三边()找直角()找夹角(已知两边AASASAASAAASSASAASSSSHLSAS精品文档---下载后可任意编辑1.判定全等三角形的方法三角形全等是证明线段相等,角相等最基本、最常用的方法,这不仅因为全等三角形有很多重要的角相等、线段相等的特征,还在于全等三角形把已知的线段相等、角相等与未知的结论联系起来。全等三角形的性质 (1)全等三角形中,对应边相等,对应角相等。 (2)全等三角形的对应线段(对应边上的中线,对应边上的高,对应角的平分线)相等。 (3)全等三角形的周长相等,面积相等。全等三角形的五种判定公理:(1)三边对应相等的两个三角形全等,“边边边”(SSS);(2)两边和它们的夹角对应相等的两个三角形全等,“边角边”(SAS);(3)两角和它们的夹边对应相等的两个三角形全等,“角边角”(ASA);(4)两个角和其中一个角的对边对应相等的两个三角形全等,“角角边”(AAS);(5)斜边和一条直角边对应相等的两个直角三角形全等,“斜边,直角边”(HL)。 SSS(边边边) SAS(边角边) ASA(角边角) AAS(角角边) HL(斜边,直角边)注意几点:(1)在判定两个三角形全等时,至少有一边对应相等;(2)以下情况两个三角形不一定全等:① 三个角对应相等的两个三角形不一定全等 (AAA)。② 两边和其中一边的对角对应相等的两个三角形不一定全等(SSA)。如图 AAA,△ABC 和△ADE 中,∠A=A∠ ,∠1=3∠ ,∠2=4∠ ,即三个角对应相等,但它们只是形状相同而大小并不相等,故它们不全等;又如图 SSA,△ABC 和△ABD中,AB=AB,AC=AD,∠B=B∠ ,即两边及其中一边的对角对应相等,但它们并不全等。寻找对应元素的规律 寻找对应边和对应角,常用到以下方法: (1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边. (2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角. (3)有公共边的,公共边是对应边. (4)有公共角的,公共角是对应角. (5)有对顶角的,对顶角是对应角. (6)如右图中,两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).通过观察,想象...