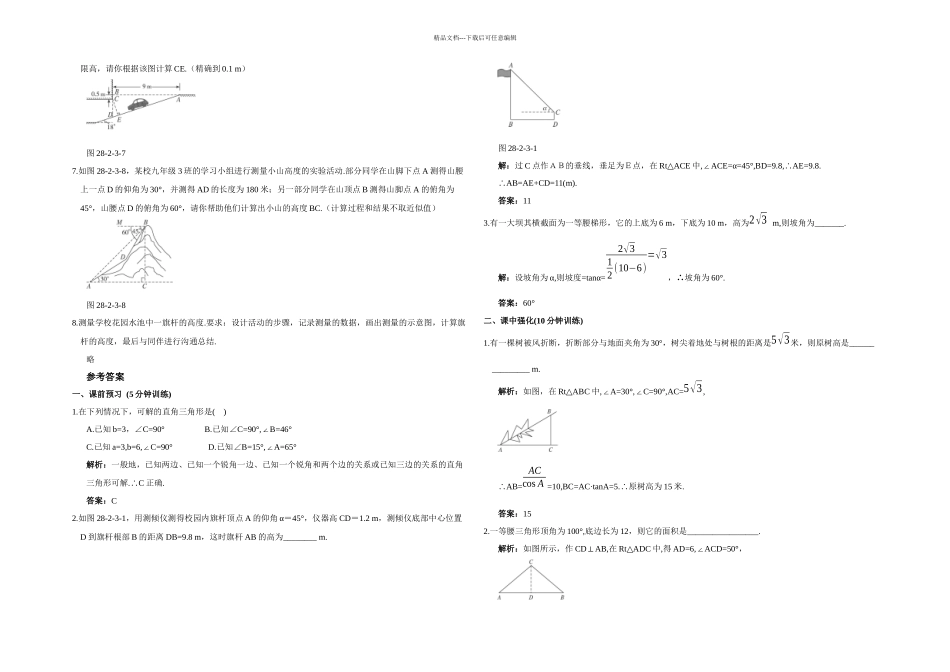
图 28-2-3-1精品文档---下载后可任意编辑一、课前预习 (5 分钟训练)1.在下列情况下,可解的直角三角形是( )A.已知 b=3,∠C=90° B.已知∠C=90°,B=46°∠C.已知 a=3,b=6,C=90° D.∠已知∠B=15°,A=65°∠2.如图 28-2-3-1,用测倾仪测得校园内旗杆顶点 A 的仰角 α=45°,仪器高 CD=1.2 m,测倾仪底部中心位置 D 到旗杆根部 B 的距离DB=9.8 m,这时旗杆 AB 的高为________ m.3.有一大坝其横截面为一等腰梯形,它的上底为 6 m,下底为10 m,高为2√3 m,则坡角为_______.二、课中强化(10 分钟训练)1.有一棵树被风折断,折断部分与地面夹角为 30°,树尖着地处与树根的距离是5√3米,则原树高是_______________ m.2.一等腰三角形顶角为 100°,底边长为 12,则它的面积是_________________.3.如图 28-2-3-2,在 Rt ABC△中,∠C=90°,AD 平分∠CAB,CD=,BD=2√3 ,求 AB 及∠B.图 28-2-3-24.如图 28-2-3-3,已知线段 AB、CD 分别表示甲、乙两幢楼的高,ABBD⊥,CDBD⊥,从甲楼顶部 A 处测得乙楼顶部 C 的仰角 α=30°,测得乙楼底部 D 的俯角 β=60°,已知甲楼高 AB=24 m,求乙楼 CD 的高.图 28-2-3-3三、课后巩固(30 分钟训练)1.菱形 ABCD 的对角线 AC 长为 10 cm,BAC=30°,∠那么 AD 为( )A.10√33 B.√33 C.15√33 D.2.在 Rt ABC△中,C=90°,CD∠是斜边 AB 上的中线,BC=4,CD=3,则∠A≈_________.3.如图 28-2-3-4 所示,为了测量河流某一段的宽度,在河北岸选了一点 A,在河南岸选相距 200 米的 B、C两点,分别测得∠ABC=60°,∠ACB=45°.求这段河的宽度.(精确到米)图 28-2-3-44.如图 28-2-3-5,山上有一座铁塔,山脚下有一矩形建筑物 ABCD,且建筑物周围没有开阔平整地带,该建筑物顶端宽度 AD 和高度 DC 都可直接测得,从 A、D、C 三点可看到塔顶端 H,可供使用的测量工具有皮尺、测倾器.(1)请你根据现有条件,充分利用矩形建筑物,设计一个测量塔顶端到地面高度 HG 的方案,具体要求如下:a.测量数据尽可能少.b.在所给图形上,画出你设计的测量平面图,并将应测数据标记在图形上.(假如测 A、D 间距离,用 m表示,若测 D、C 间的距离,用 n 表示,若测角用 α、β、γ 表示)(2)根据你测量的数据,计算塔顶端到地面的高度 HG.(用字母表示,测倾器高度忽略不计)图 28-2-3-55.如图 28-2-3-6,高速公路路基的横断面为梯形,...