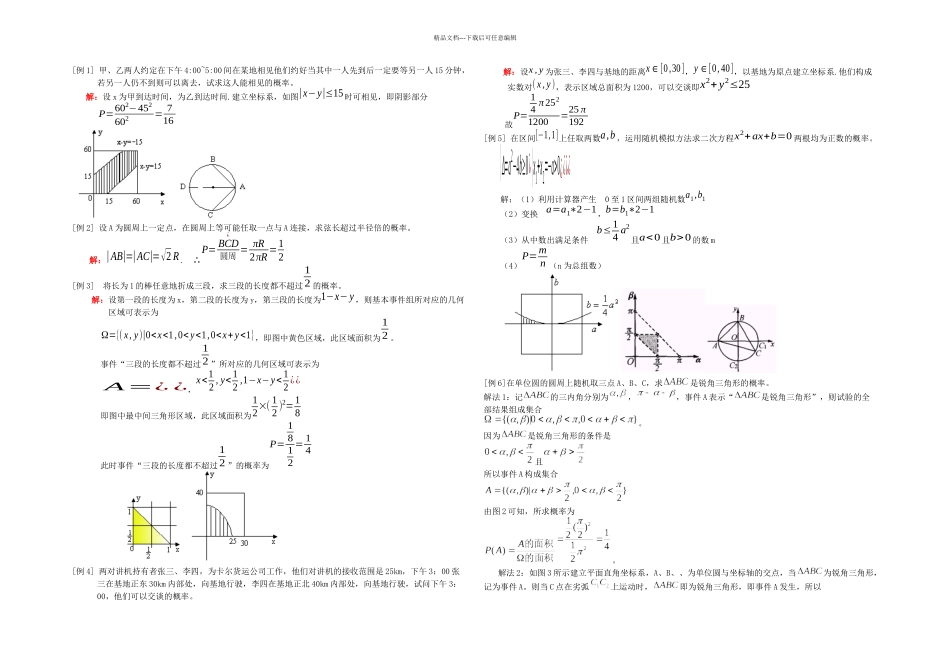
精品文档---下载后可任意编辑[例 1] 甲、乙两人约定在下午 4:00~5:00 间在某地相见他们约好当其中一人先到后一定要等另一人 15 分钟,若另一人仍不到则可以离去,试求这人能相见的概率。解:设 x 为甲到达时间,为乙到达时间.建立坐标系,如图|x−y|≤15时可相见,即阴影部分P=602−452602= 716[例 2] 设 A 为圆周上一定点,在圆周上等可能任取一点与 A 连接,求弦长超过半径倍的概率。解:|AB|=|AC|=√2 R. ∴P= BCD¿圆周 = πR2πR=12[例 3] 将长为 1 的棒任意地折成三段,求三段的长度都不超过12 的概率。解:设第一段的长度为 x,第二段的长度为 y,第三段的长度为1−x− y ,则基本事件组所对应的几何区域可表示为Ω={( x, y)|00¿¿¿¿解:(1)利用计算器产生 0 至 1 区间两组随机数a1,b1(2)变换 a=a1∗2−1,b=b1∗2−1(3)从中数出满足条件 b≤14 a2且a<0 且b>0 的数 m(4)P=mn (n 为总组数)[例 6]在单位圆的圆周上随机取三点 A、B、C,求是锐角三角形的概率。解法 1:记的三内角分别为,,事件 A 表示“是锐角三角形”,则试验的全部结果组成集合。因为是锐角三角形的条件是且所以事件 A 构成集合由图 2 可知,所求概率为。解法 2:如图 3 所示建立平面直角坐标系,A、B、、为单位圆与坐标轴的交点,当为锐角三角形,记为事件 A。则当 C 点在劣弧上运动时,即为锐角三角形,即事件 A 发生,所以P例 9 图DCBA精...