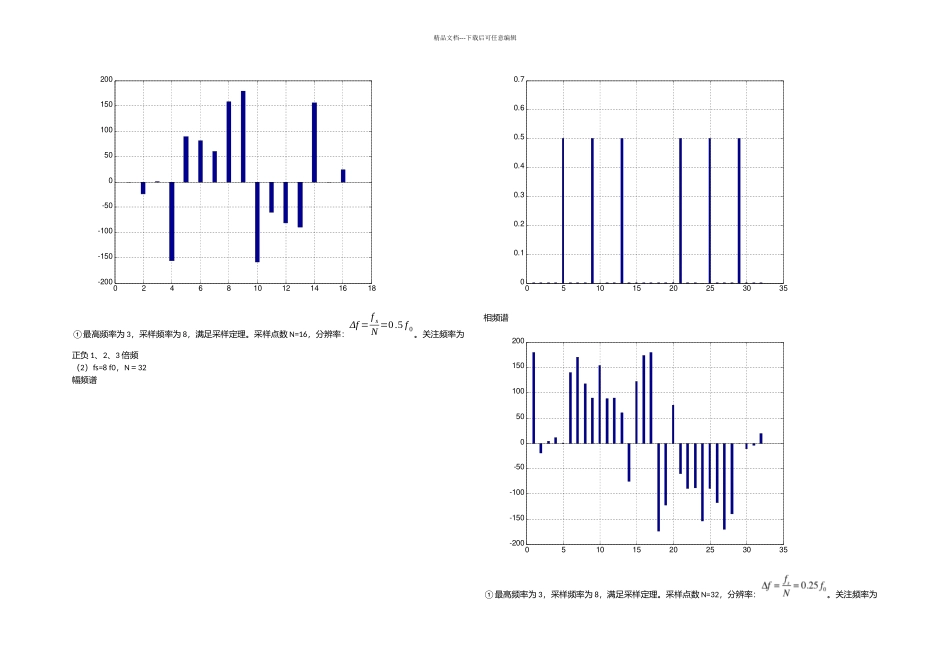
精品文档---下载后可任意编辑2024010541 机 14 林志杭一、实验目的 1.加深对几个特别概念的理解:“采样”……“混叠”;“窗函数”(截断)……“泄漏”;“非整周期截取”……“栅栏”。 2.加深理解如何才能避开“混叠”,减少“泄漏”,防止“栅栏”的方法和措施以及估量这些因素对频谱的影响。3.对利用通用微型计算机及相应的 FFT 软件,实现频谱分析有一个初步的了解。二、实验原理为了实现信号的数字化处理,利用计算机进行频谱分析――计算信号的频谱。由于计算机只能进行有限的离散计算(即 DFT),因此就要对连续的模拟信号进行采样和截断。而这两个处理过程可能引起信号频谱的畸变,从而使 DFT 的计算结果与信号的实际频谱有误差。有时由于采样和截断的处理不当,使计算出来的频谱完全失真。因此在时域处理信号时要格外小心。时域采样频率过低,将引起频域的“混叠”。为了避开产生“混叠”,要求时域采样时必须满足采样定理,即:采样频率 fs 必须大于信号中最高频率 fc 的 2 倍(fs>2fc)。因此在信号数字处理中,为避开混叠,依不同的信号选择合适的采样频率将是十分重要的。频域的“泄漏”是由时域的截断引起的。时域的截断使频域中原来集中的能量向它的邻域扩散(如由一个δ(f)变成一个 sinc(f),而泄漏的旁瓣将影响其它谱线的数值。时域截断还会引起“栅栏效应”,对周期信号而言,它是由于截断长度不等于周期信号的周期的整数倍而引起的。因此避开“栅栏”效应的办法就是整周期截断。综上所述,在信号数字化处理中应十分注意以下几点:1.为了避开“混叠”,要求在采样时必须满足采样定理。为了减少“泄漏”,应适当增加截断长度和选择合适的窗对信号进行整周期截取,则能消除“栅栏数应”。增加截断长度,则可提高频率分辨率。三、预习内容熟悉 Matlab 语言、函数和使用方法;利用 Matlab 所提供的 FFT 函数编写程序。四、实验内容及步骤调通所编写的程序,对下列信号〔函数〕进行离散 FFT 变换,根据题目的要求……FFT 变换点数〔截断长度〕及采样频率,计算各点的傅里叶变换值,画出频谱图,对典型的谱线标出其幅值及相角。(-)内容:1.x(t )=sin(ω0t + π6 )+sin2ω0t+cos3ω0 t代码:N=input('N=');n=input('n=');t=1:1:N;w=2*pi;x1=sin(w*(t-1)/n+pi/6)+sin(2*w*(t-1)/n)+cos(3*w*(t-1)/n);y=fft(x1);y=fftshift(y);an=angle(y)/pi*180;y=abs(y)/N;figure(1);bar(t,y,0.3);grid...