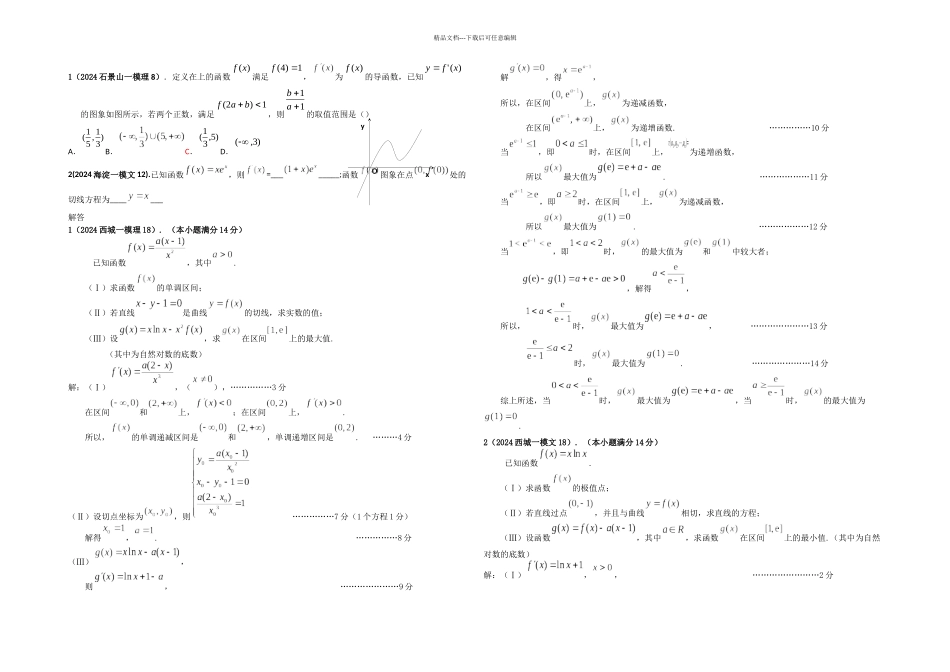
xyO精品文档---下载后可任意编辑1(2024 石景山一模理 8).定义在上的函数满足,为的导函数,已知的图象如图所示,若两个正数,满足,则的取值范围是()A.B.C.D.2(2024 海淀一模文 12).已知函数,则=________;函数图象在点处的切线方程为_______解答1(2024 西城一模理 18). (本小题满分 14 分)已知函数,其中.(Ⅰ)求函数的单调区间;(Ⅱ)若直线是曲线的切线,求实数的值;(Ⅲ)设,求在区间上的最大值.(其中为自然对数的底数)解:(Ⅰ),(),……………3 分在区间和上,;在区间上,.所以,的单调递减区间是和,单调递增区间是. ………4 分(Ⅱ)设切点坐标为,则 ……………7 分(1 个方程 1 分)解得,. ……………8 分(Ⅲ),则, …………………9 分解,得,所以,在区间上,为递减函数,在区间上,为递增函数. ……………10 分当,即时,在区间上,τ(a1,a2,⋯,an)=为递增函数,所以最大值为. ………………11 分当,即时,在区间上,为递减函数,所以最大值为. ………………12 分当,即时,的最大值为和中较大者;,解得,所以,时,最大值为, …………………13 分时,最大值为. …………………14 分综上所述,当时,最大值为,当时,的最大值为.2(2024 西城一模文 18). (本小题满分 14 分)已知函数.(Ⅰ)求函数的极值点;(Ⅱ)若直线过点,并且与曲线相切,求直线的方程;(Ⅲ)设函数,其中,求函数在区间上的最小值.(其中为自然对数的底数)解:(Ⅰ),, ……………………2 分)(xf1)4(f)(xf)(' xfy 1)2( baf11ab)31,51()5,31()3,(精品文档---下载后可任意编辑由得,……………………3 分所以,在区间上单调递减,在区间上单调递增. ………………4 分所以,是函数的微小值点,极大值点不存在. …………………5 分(Ⅱ)设切点坐标为,则, …………………6 分切线的斜率为,所以,, …………………7 分解得,, …………………8 分所以直线的方程为. …………………9 分(Ⅲ),则, …………………10 分解,得,所以,在区间上,为递减函数,在区间上,为递增函数. …………………11 分当,即时,在区间上,为递增函数,所以最小值为. …………………12 分当,即时,的最小值为. ……………13 分当,即时,在区间上,为递减函数,所以最小值为. ………………14 分 综上,当时,最小值为;当时,的最小值;当时,的最小...