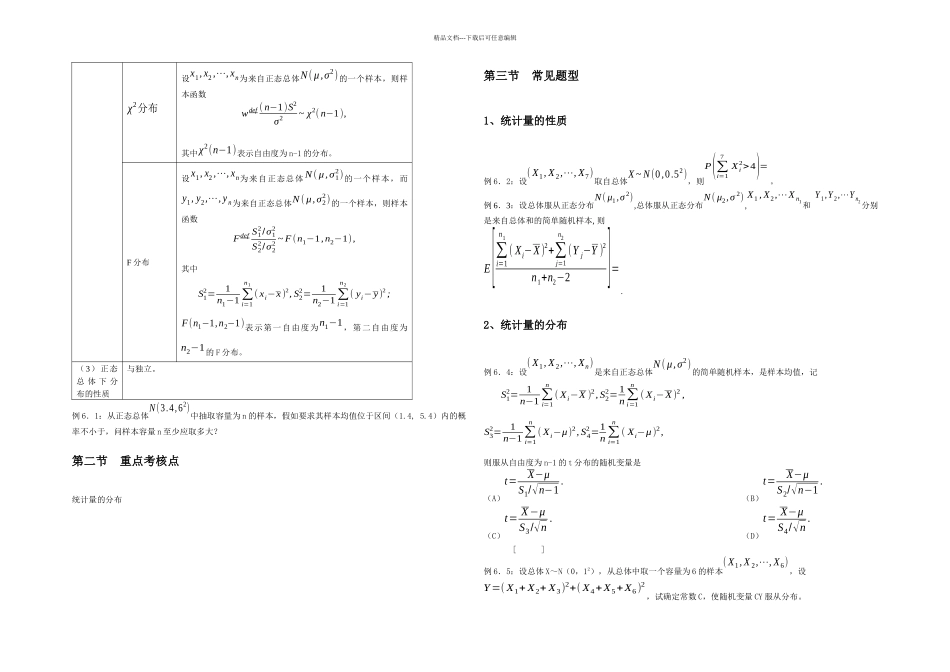
精品文档---下载后可任意编辑第一节 基本概念1、概念网络图数理统计的基本概念{总体个体样本样本函数统计量 }→正态总体下的四大分布2、重要公式和结论(1)数理统 计 的 基本概念总体在数理统计中,常把被考察对象的某一个(或多个)指标的全体称为总体(或母体)。我们总是把总体看成一个具有分布的随机变量(或随机向量)。个体总体中的每一个单元称为样品(或个体)。样本我们把从总体中抽取的部分样品x1, x2 ,⋯, xn称为样本。样本中所含的样品数称为样本容量,一般用 n 表示。在一般情况下,总是把样本看成是 n 个相互独立的且与总体有相同分布的随机变量,这样的样本称为简单随机样本。在泛指任一次抽取的结果时,x1, x2 ,⋯, xn表示 n 个随机变量(样本);在具体的一次抽取之后,x1, x2 ,⋯, xn表示 n 个具体的数值(样本值)。我们称之为样本的两重性。样本函数和统计量设x1, x2 ,⋯, xn为总体的一个样本,称ϕ=ϕ (x1, x2 ,⋯, xn)为样本函数,其中为一个连续函数。假如中不包含任何未知参数,则称(x1, x2 ,⋯, xn)为一个统计量。常见统计量及其性质样本均值x=1n∑i=1nxi.样本方差S2=1n−1∑i=1n( xi−x )2.样本标准差S=√1n−1∑i=1n( xi−x)2.样本 k 阶原点矩M k=1n∑i=1nxik,k=1,2,⋯.样本 k 阶中心矩M k' =1n∑i=1n(xi−x)k ,k=2,3,⋯.E( X)=μ ,D( X )=σ2n ,E( S2)=σ2,E( S∗2)=n−1nσ2,其中S∗2¿ 1n∑i=1n( Xi−X)2,为二阶中心矩。(2)正态总 体 下 的四大分布正态分布设x1, x2 ,⋯, xn为来自正态总体N( μ,σ2)的一个样本,则样本函数udef x−μσ/√n~N(0 ,1).t 分布设x1, x2 ,⋯, xn为来自正态总体N( μ,σ2)的一个样本,则样本函数tdef x−μ√S2n~t (n−1),其中 t(n-1)表示自由度为 n-1 的 t 分布。精品文档---下载后可任意编辑χ2分布设x1, x2 ,⋯, xn为来自正态总体N( μ,σ2)的一个样本,则样本函数wdef ( n−1)S2σ2~ χ2( n−1),其中χ2(n−1)表示自由度为 n-1 的分布。F 分布设x1, x2 ,⋯, xn为来自正态总体N ( μ,σ12)的一个样本,而y1, y2,⋯, y n为来自正态总体N ( μ,σ22)的一个样本,则样本函数Fdef S12/σ12S22/σ22 ~ F (n1−1,n2−1),其中S12=1n1−1∑i=1n1( xi−x)2, S22=1n2−1∑i=1n2( yi−y)2;F(n1−1,n2−1)表示第一自由度为n1−1,第二自由度为n2−1 的 F 分布。(3)正态总...