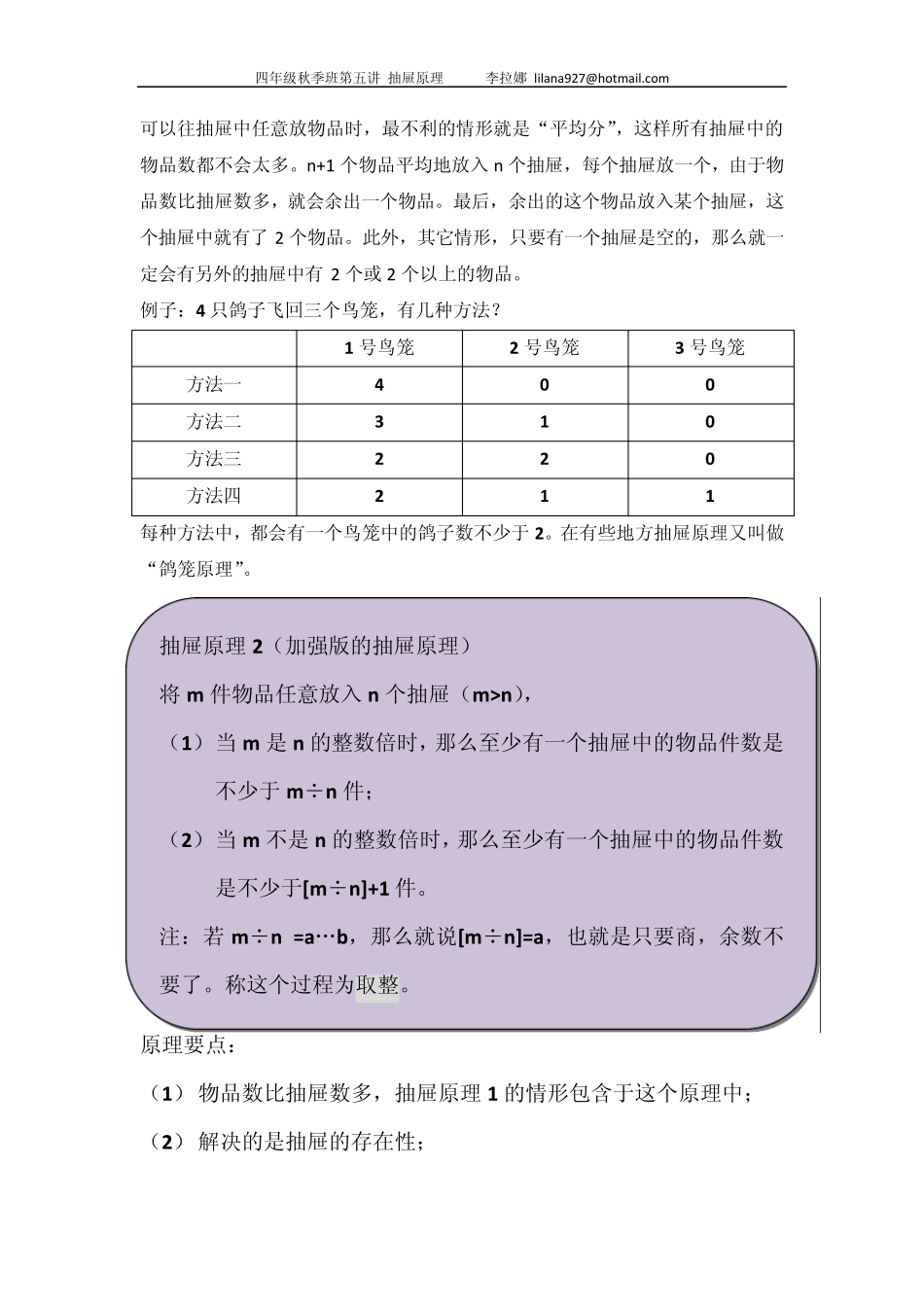
四年级秋季班第五讲 抽屉原理 李拉娜 lilana927@hotmail.com 第五讲 简单抽屉原理、最不利原则 知识框架 一、 对抽屉原理两个版本的认识 原理要点: (1) 物品数比抽屉数多1。只有物品数比抽屉数多时抽屉原理才会成立。 (2) 物品是“任意放”到抽屉中。 (3) 其中“物品不少于 2 件”的抽屉是一定存在的,但是不确定是哪一个。 (4) 原理的结论是:“至少有一个抽屉中的物品数不少于 2 件”,也可以这么说,“至少有2 件物品在同一个抽屉中”。 原理讲解: 只要有一个抽屉中的物品数不少于 2 件,抽屉原理1 就是成立的。当我们抽屉原理1:将 n+1 个物品任意放到 n 个抽屉中,那么至少有一个抽屉中的物品不少于 2 件。 四年级秋季班第五讲 抽屉原理 李拉娜 lilana927@hotmail.com 可以往抽屉中任意放物品时,最不利的情形就是“平均分”,这样所有抽屉中的物品数都不会太多。n+1 个物品平均地放入n 个抽屉,每个抽屉放一个,由于物品数比抽屉数多,就会余出一个物品。最后,余出的这个物品放入某个抽屉,这个抽屉中就有了2 个物品。此外,其它情形,只要有一个抽屉是空的,那么就一定会有另外的抽屉中有2 个或2 个以上的物品。 例子:4 只鸽子飞回三个鸟笼,有几种方法? 1 号鸟笼 2 号鸟笼 3 号鸟笼 方法一 4 0 0 方法二 3 1 0 方法三 2 2 0 方法四 2 1 1 每种方法中,都会有一个鸟笼中的鸽子数不少于2。在有些地方抽屉原理又叫做“鸽笼原理”。 原理要点: (1) 物品数比抽屉数多,抽屉原理1 的情形包含于这个原理中; (2) 解决的是抽屉的存在性; 抽屉原理2(加强版的抽屉原理) 将m 件物品任意放入n个抽屉(m>n), (1) 当m 是n的整数倍时,那么至少有一个抽屉中的物品件数是不少于m÷n件; (2) 当m 不是n的整数倍时,那么至少有一个抽屉中的物品件数是不少于[m÷n]+1 件。 注:若 m÷n =a„b,那么就说[m÷n]=a,也就是只要商,余数不要了。称这个过程为取整。 四年级秋季班第五讲 抽屉原理 李拉娜 lilana927@hotmail.com (3) 在解题时,遇到“有一个抽屉中的物品数不少于A 件”,其中A>2 时,应使用抽屉原理2。 (4) 原理的结论也可以理解为:“总有不少于m÷n件(或[m÷n]+1件)物品在同一个抽屉中。”相同的即为“抽屉”。 原理讲解: 最不利的情形就是“平均分”,这样每个抽屉中的物品数都不太多都是[m÷n]个。若 m...