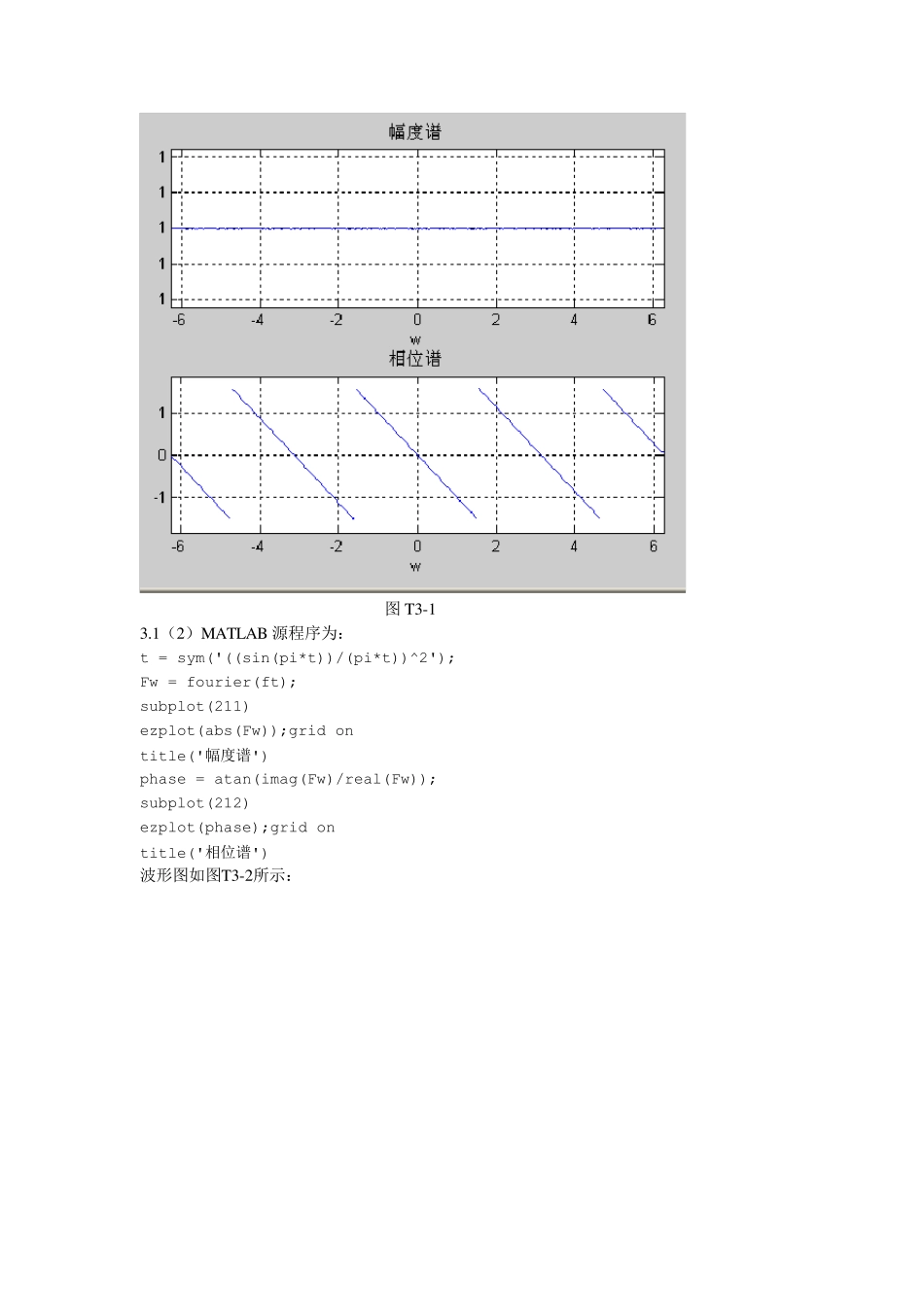
信息工程学院实验报告 课程名称:信号与系统 实验项目名称:实验3 傅里叶变换及其性质 实验时间:2013.11.29 实 验 目 的: 学会运用MATLAB 求连续时间信号的傅里叶(Fourier)变换;学会运用MATLAB 求连续时间信号的频谱图;学会运用MATLAB 分析连续时间信号的傅里叶变换的性质。 实 验 环 境: Windows 7 MATLAB7.1 实 验 内 容 及 过 程: 3.1 试用MATLAB 命令求下列信号的傅里叶变换,并绘出其幅度谱和相位谱。 (1)1sin 2 (1)( )(1)tf tt (2)22sin()( )tf tt 3.2 试用MATLAB 命令求下列信号的傅里叶反变换,并绘出其时域信号图。 (1)1104( )35Fjj (2)224( )Fe 3.3 试用MATLAB 数值计算方法求门信号的傅里叶变换,并画出其频谱图。 门信号即1,/ 2( )0,/ 2tg tt ,其中1 。 3.4 已知两个门信号的卷积为三角波信号,试用MATLAB 命令验证傅里叶变换 的时域卷积定理。 3.1(1)MATLAB 源程序为: ft = sym('(sin(2*pi*(t-1)))/(pi*(t-1))'); Fw = fourier(ft); subplot(211) ezplot(abs(Fw));grid on title('幅度谱') phase = atan(imag(Fw)/real(Fw)); subplot(212) ezplot(phase);grid on title('相位谱') 波形图如图T3-1所示: 成 绩: 指导教师(签名): 图T3-1 3.1(2)MATLAB 源程序为: t = sym('((sin(pi*t))/(pi*t))^2'); Fw = fourier(ft); subplot(211) ezplot(abs(Fw));grid on title('幅度谱') phase = atan(imag(Fw)/real(Fw)); subplot(212) ezplot(phase);grid on title('相位谱') 波形图如图T3-2所示: 图T3-2 3.2(1)MATLAB 源程序为: t=sym('t'); Fw = sym('10/(3+i*w)-4/(5+i*w)'); ft = ifourier(Fw); ezplot(ft); grid on; axis([-1 3 -1 7]); 波形图如图T3-3所示: 图T3-3 3.2(2)MATLAB 源程序为: t=sym('t'); Fw = sym('exp(-4*w^2)'); ft = ifourier(Fw); ezplot(ft) grid on 波形图如图T3-4所示: 图T3-4 3.3、MATLAB 源程序为: dt = 0.001; t = -0.5:dt:0.5; ft = uCT(t+0.5)-uCT(t-0.5); N = 2000; k = -N:N; W = 2*pi*k/((2*N+1)*dt); F = dt * ft*exp(-j*t'*W); plot(W,F);grid on; axis([-pi pi -1 3]); xlabel('W'), ylabel('F(W)') title('amplitude spectrum'); 波形图如图T3-5所示: 图T3-5 3.4 将门函数先进行时域卷积运算,再将卷积后的结果做傅里叶变换,程序和结果如下: clear;clc; dt = 0.01; t = -2:dt:2.5; f1 = uCT(t+0.5)- uCT(t-0.5); f = conv(f1,f1)*dt; ft=sym('f'); Fw = fourier(ft) Fw =2*i*pi*dirac(1,w) 将一个门函数先进行傅里叶变换,再将结果与自身相乘,程序和结果如下: clear;clc; dt = 0.01; t = -2:dt:2.5; f1 = uCT(t+0.5)- uCT(t-0.5); ft=sym('f1'); Fw = fourier(ft); Fw=Fw*Fw Fw =-4*pi^2*dirac(1,w)^2 由此来验证傅里叶变换的时域卷积定理