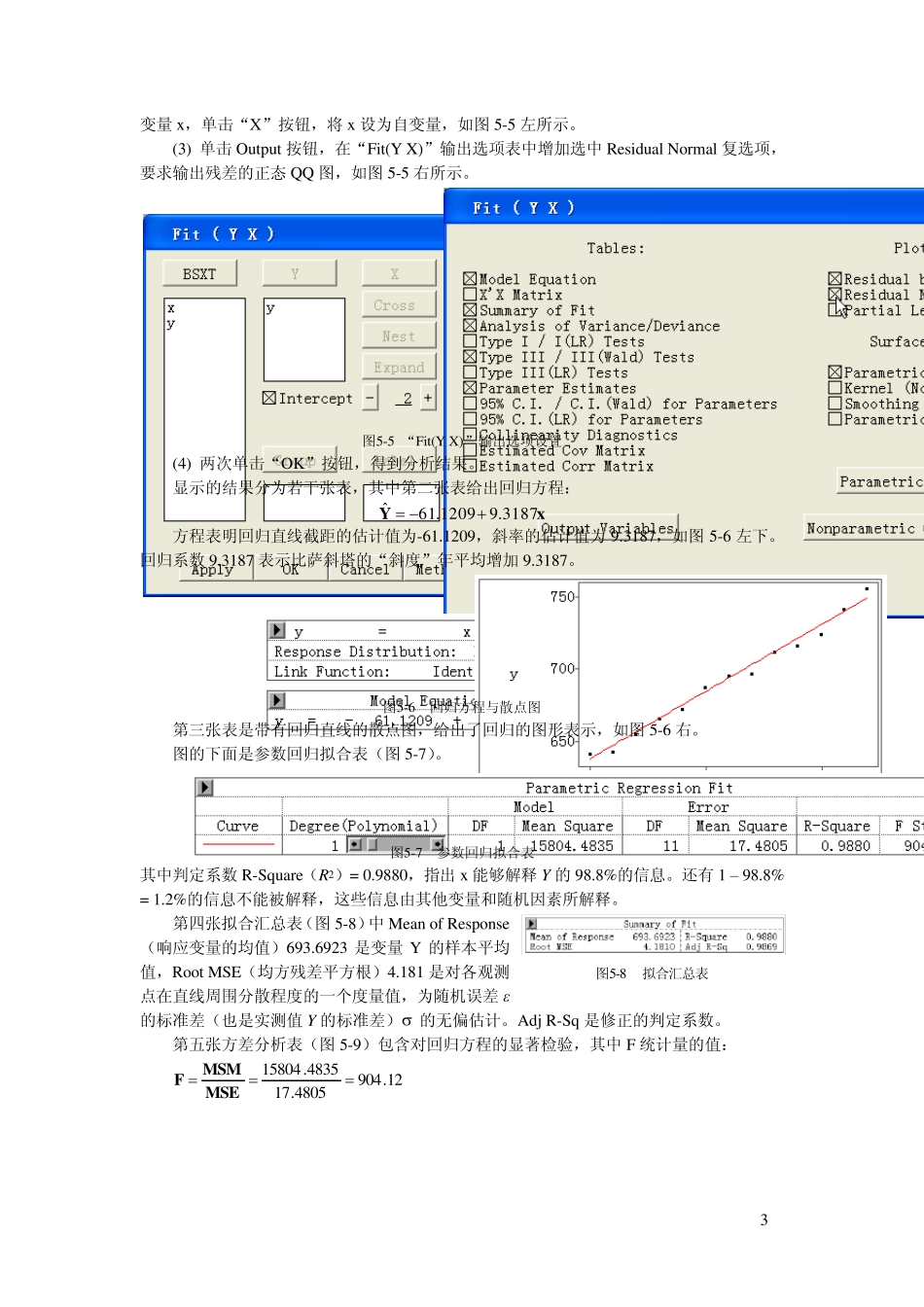
1 实验五 相关和回归分析 相关分析是指对变量之间的相关关系进行描述与度量的一种分析方法,简单相关分析通常指对两变量间相关关系的研究,其目的是确定两个变量之间是否存在相关关系,并对其相关关系的强度进行度量,常用方法是考察两个变量的散点图和计算变量间的相关系数。 多元线性回归分析研究多个变量的数量伴随关系,内容主要包括模型的假定与检验、参数的估计与检验、回归诊断与预测。 很多非线性回归问题都可以转化为线性回归问题处理,如多项式回归、指数回归、对数回归、幂函数回归等。 5.1 实验目的 掌握使用SAS 进行简单相关分析和多元线性回归分析及非线性回归分析的方法。 5.2 实验内容 一、用INSIGHT 模块作简单相关分析与一元线性回归分析 二、用“分析家”作多元线性回归分析 三、使用REG 过程作回归分析 四、一元非线性回归分析 5.3 实验指导 一、用 INSIGHT 模块作简单相关分析与一元线性回归分析 【实验5-1】比萨斜塔是一建筑奇迹,工程师关于塔的稳定性作了大量研究工作,塔的斜度的测量值随时间变化的关系提供了很多有用的信息,表 5-1 给出了 1975 年至 1987 年的测量值(sy5_1.xls)。表中变量“斜度”表示塔上某一点的实际位置与假如塔为垂直时它所处位置之偏差再减去 2900mm。 表 5-1 比萨斜塔的斜度 年份 x 75 76 77 78 79 80 81 82 83 84 85 86 87 斜度y(1/10mm) 642 644 656 667 673 688 696 698 713 717 725 742 757 试分析y(斜度)关于年份 x 的相关关系,写出 y 关于 x 的线性回归方程,并利用所建回归方程预测1988 年时比萨斜塔的斜度值。 1. 数据的导入 首先将上表在Excel 中处理后导入成 SAS 数据集 Mylib.sy5_1,如图5-1 所示,其中 x表示年份 y 表示斜度。 2 2. 制作散点图 制作斜度y 与年份x 的散点图,以便判断变量之间的相关性。步骤如下: (1) 在INSIGHT 中打开数据集Mylib.sy5_1。 (2) 选择菜单“Analyze(分析)”→“Scatter Plot (Y X)(散点图)”。 (3) 在打开的“Scatter Plot (Y X)”对话框中选定 Y 变量:Y;选定 X 变量:x,如图5-2 左所示。 (4) 单击“OK”按钮,得到斜度y 与年份x 的散点图,如图5-2 右所示。 从散点图中可以看出,斜度y 与年份x 之间具有一定的线性关系。 图5-2 斜度y与年份x的散点图 3. 相关系数计算 在INSIGHT 中打开数据集Mylib.sy5_1。 (1)...