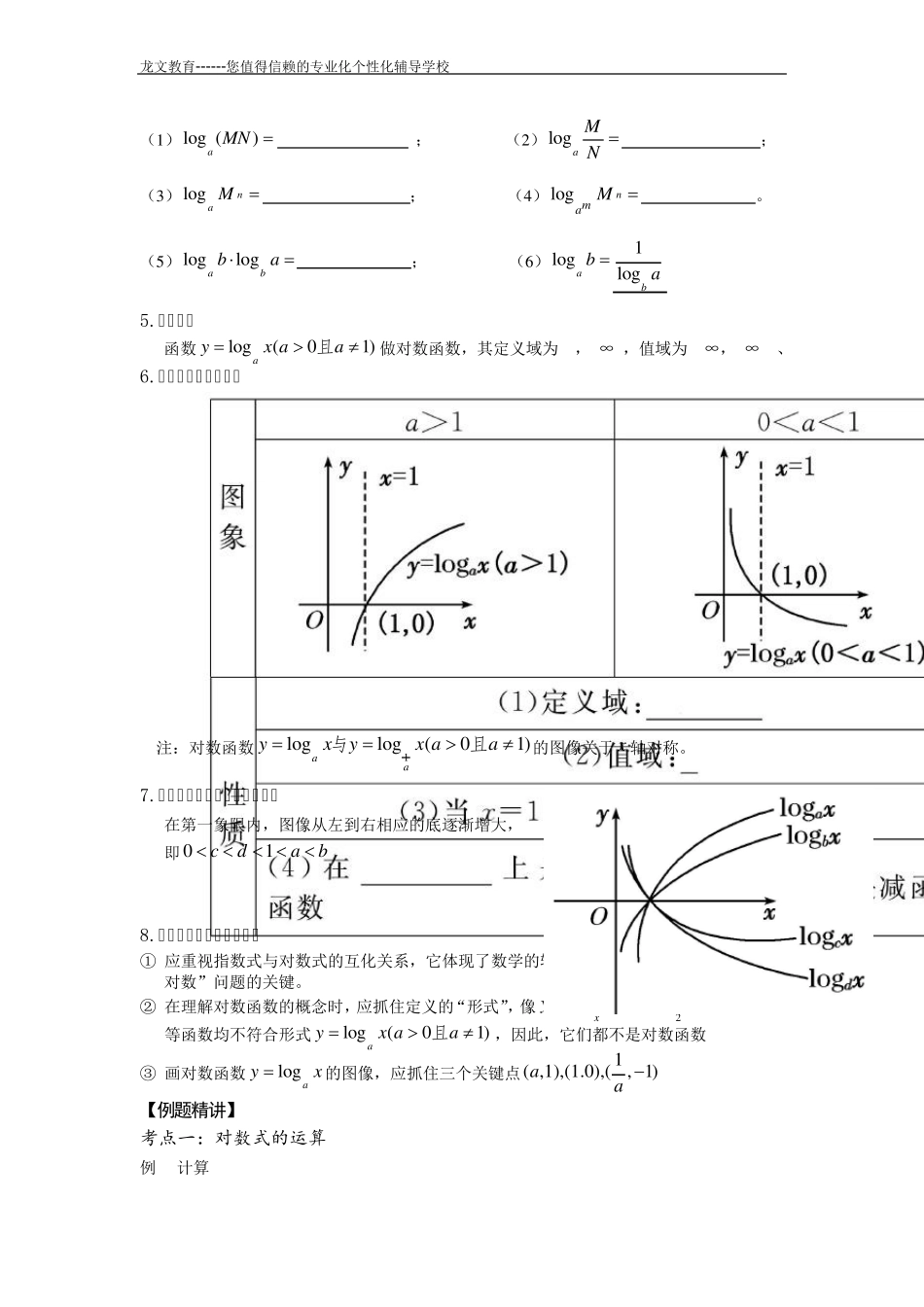
龙文教育------您值得信赖的专业化个性化辅导学校 一、教学目标: 1.理解对数的概念,掌握对数的运算性质; 2.掌握对数函数的概念、图象和性质;能利用对数函数的性质解题. 二、教学重、难点: 运用对数运算性质进行求值、化简、证明、运用对数函数的定义域、单调性解题 三、命题规律: 主要考察指数式baN与对数式lo ga Nb的互化,对数函数的图像和性质或由对数函数复合成的函数,主要涉及比较大小、奇偶性、过定点、单调区间以及运用单调性求最值等,主要以填空为主。 四、教学内容: 【知识回顾】 1.对数的概念 如果 ,那么数b 叫做以a 为底N的对数,记作 ,其中a叫做对数的 ,N叫做对数的 。 即指数式与对数式的互化:lo gbaaNbN 2.常用对数:通常将以10为底的对数10lo gN 叫做常用对数,记作lg N 。 自然对数:通常将以无理数2.71828e 为底的对数叫做自然对数,记作ln N 。 3.对数的性质及对数恒等式、换底公式 (1)对数恒等式:①lo gNaa= (01,0)aaN且② lo gNa a= (01,0)aaN且 (2)换底公式:lo ga N lo glo gbbNa (3)对数的性质:①负数和零没有对数 ② 1的对数是零,即lo g 10a ③底的对数等于 1,即lo g1a a ④lo glo glo gabcbcd lo ga d 4.对数的运算性质 如果01,0,0aaMN且,那么 龙文教育------您值得信赖的专业化个性化辅导学校 (1)lo g ()a MN ; (2)lo gaMN ; (3)lo gna M ; (4)lo gnam M 。 (5)lo glo gabba ; (6)lo ga b 1lo gb a 5.对数函数 函数lo g(01)ayx aa且做对数函数,其定义域为(0,+∞),值域为(-∞,+∞).、 6.对数函数图像与性质 注:对数函数1lo glo g(01)aayxyx aa与且的图像关于x 轴对称。 7.同真数的对数值大小关系如图 在第一象限内,图像从左到右相应的底逐渐增大, 即01cdab 8.对数式、对数函数的理解 ① 应重视指数式与对数式的互化关系,它体现了数学的转化思想,也往往是解决“指数、对数”问题的关键。 ② 在理解对数函数的概念时,应抓住定义的“形式”,像2lo g 2,lo g 2 ,3lnxyyx yx等函数均不符合形式lo g(01)ayx aa且,因此,它们都不是对数函数 ③ 画对数函数lo gayx的图像,应抓住三个关键点1( ,1),(1.0),(, 1)aa 【例...