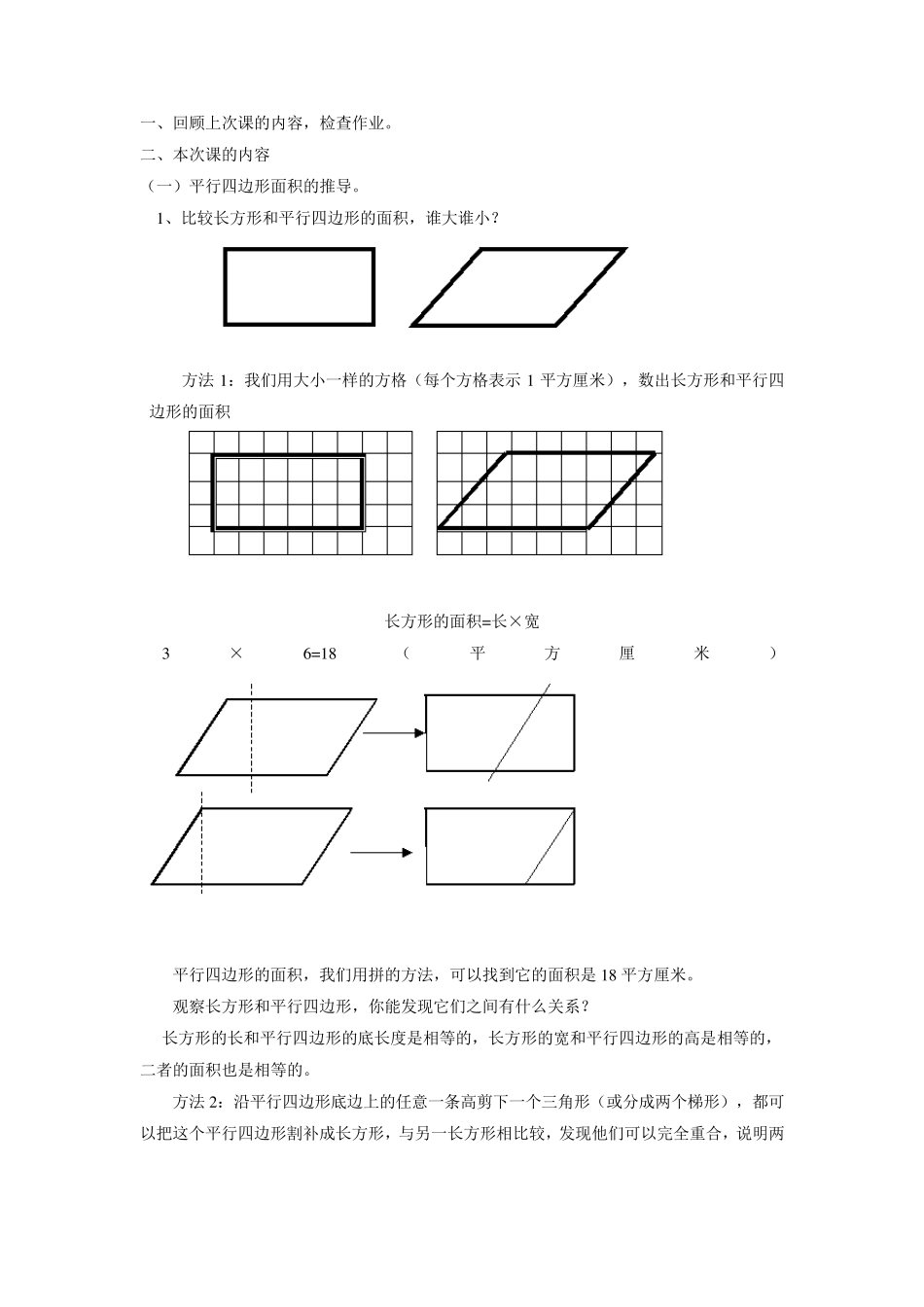
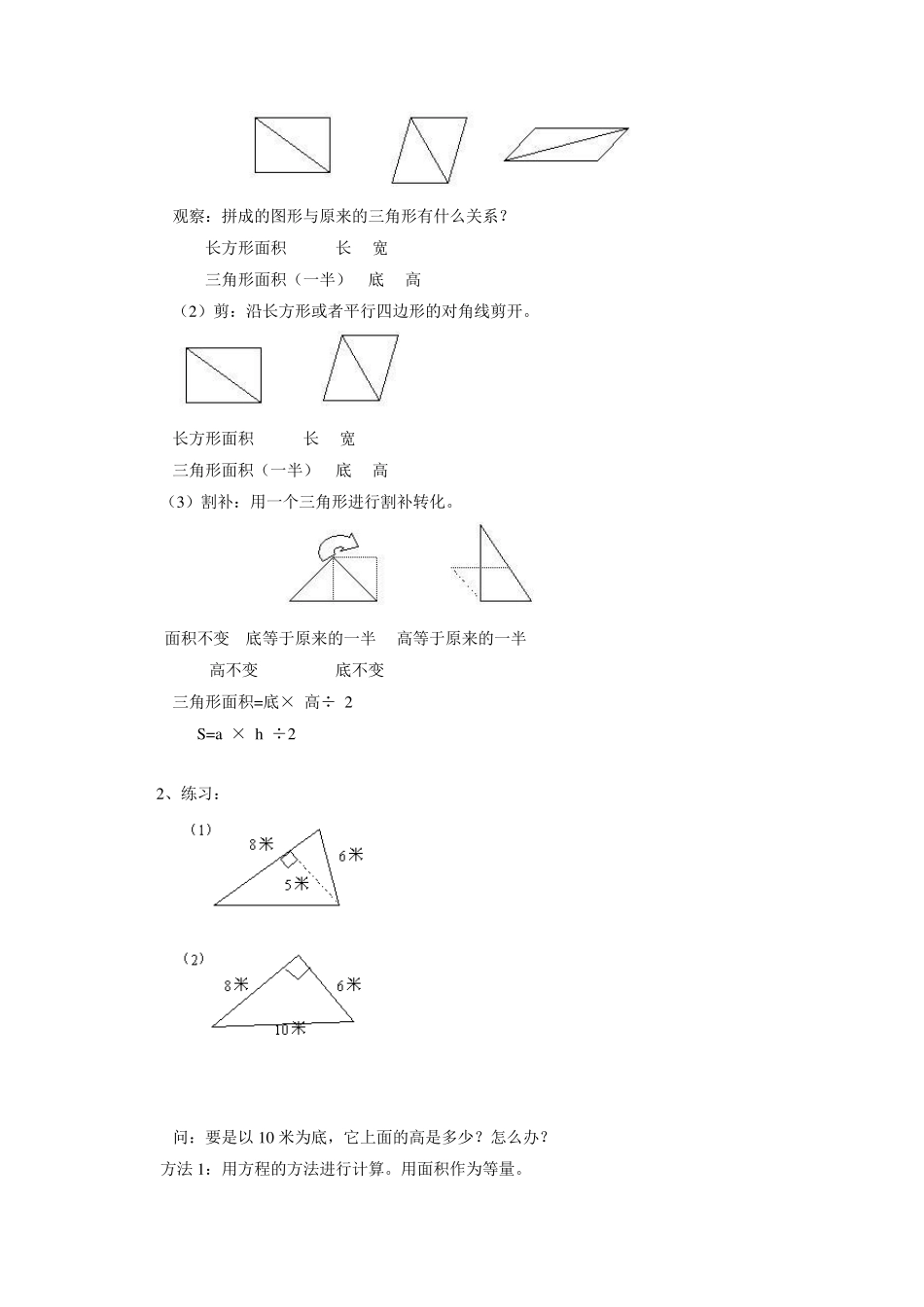
一、回顾上次课的内容,检查作业。 二、本次课的内容 (一)平行四边形面积的推导。 1、比较长方形和平行四边形的面积,谁大谁小? 方法1:我们用大小一样的方格(每个方格表示1 平方厘米),数出长方形和平行四边形的面积 长方形的面积=长×宽 3×6=18( 平 方 厘 米 ) 平行四边形的面积,我们用拼的方法,可以找到它的面积是 18 平方厘米。 观察长方形和平行四边形,你能发现它们之间有什么关系? 长方形的长和平行四边形的底长度是相等的,长方形的宽和平行四边形的高是相等的,二者的面积也是相等的。 方法2:沿平行四边形底边上的任意一条高剪下一个三角形(或分成两个梯形),都可以把这个平行四边形割补成长方形,与另一长方形相比较,发现他们可以完全重合,说明两个图形的面积是相等的。还发现长方形的长等于原平行四边形的底,长方形宽等于原平行四边形的高。 通过以上的操作,我们同学都认识到平行四边形的面积与长方形的面积有内在的联系,我们总不能都把平行四边形割补成长方形来进行计算。那就需要我们找到一种解决平行四边形面积计算的方法?怎样计算平行四边形的面积呢? 长 方 形 的面积= 长 × 宽 平行四边形的面积= 底 × 高 S= a h 练习: 1、在空格里填上适当的数 底(厘米) 5 10 0.7 高(厘米) 8 0.5 2.5 面积(平方厘米) 0.42 10 2、求下列图形的面积(单位:厘米) (二)三角形的面积。 1、我们用割补的方法,将平行四边形的面积转化成以前学习过的长方形,找到他们之间的关系就可以推导出平行四边形的面积了。 我们现在要研究三角形的面积,同学们可以将三角形转化成什么图形,然后再找关系,推导出三角形的面积计算方法呢?(长方形、平行四边形) (1)拼:用两个完全一样的三角形拼成平行四边形或者长方形。 观察:拼成的图形与原来的三角形有什么关系? 长方形面积 长 宽 三角形面积(一半) 底 高 (2)剪:沿长方形或者平行四边形的对角线剪开。 长方形面积 长 宽 三角形面积(一半) 底 高 (3)割补:用一个三角形进行割补转化。 面积不变 底等于原来的一半 高等于原来的一半 高不变 底不变 三角形面积=底× 高÷ 2 S=a × h ÷2 2、练习: 问:要是以 10 米为底,它上面的高是多少?怎么办? 方法 1:用方程的方法进行计算。用面积作为等量。 方法2: (3)下图中的哪个三角形面积与涂色三角形的面积相等。 小...