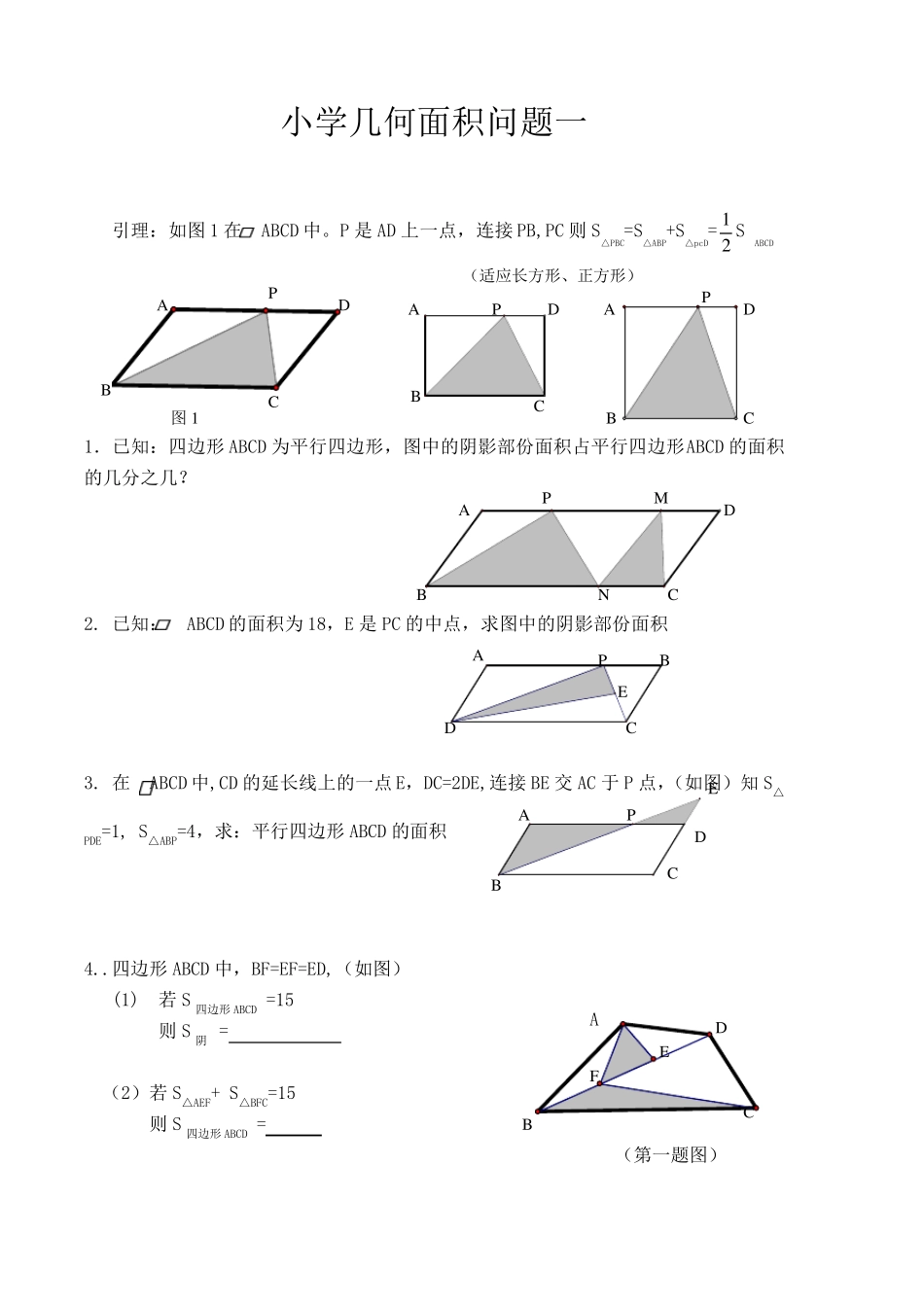
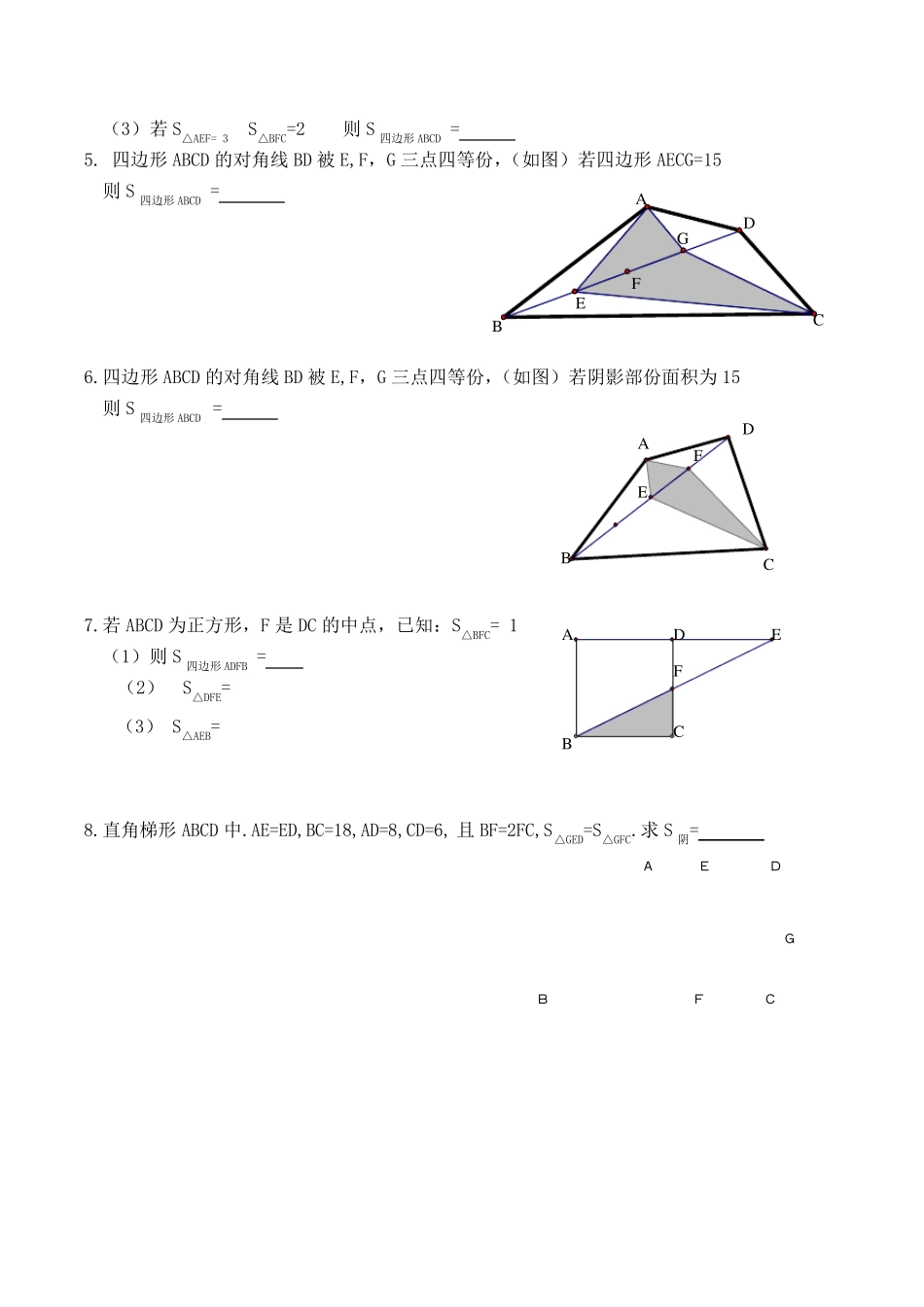
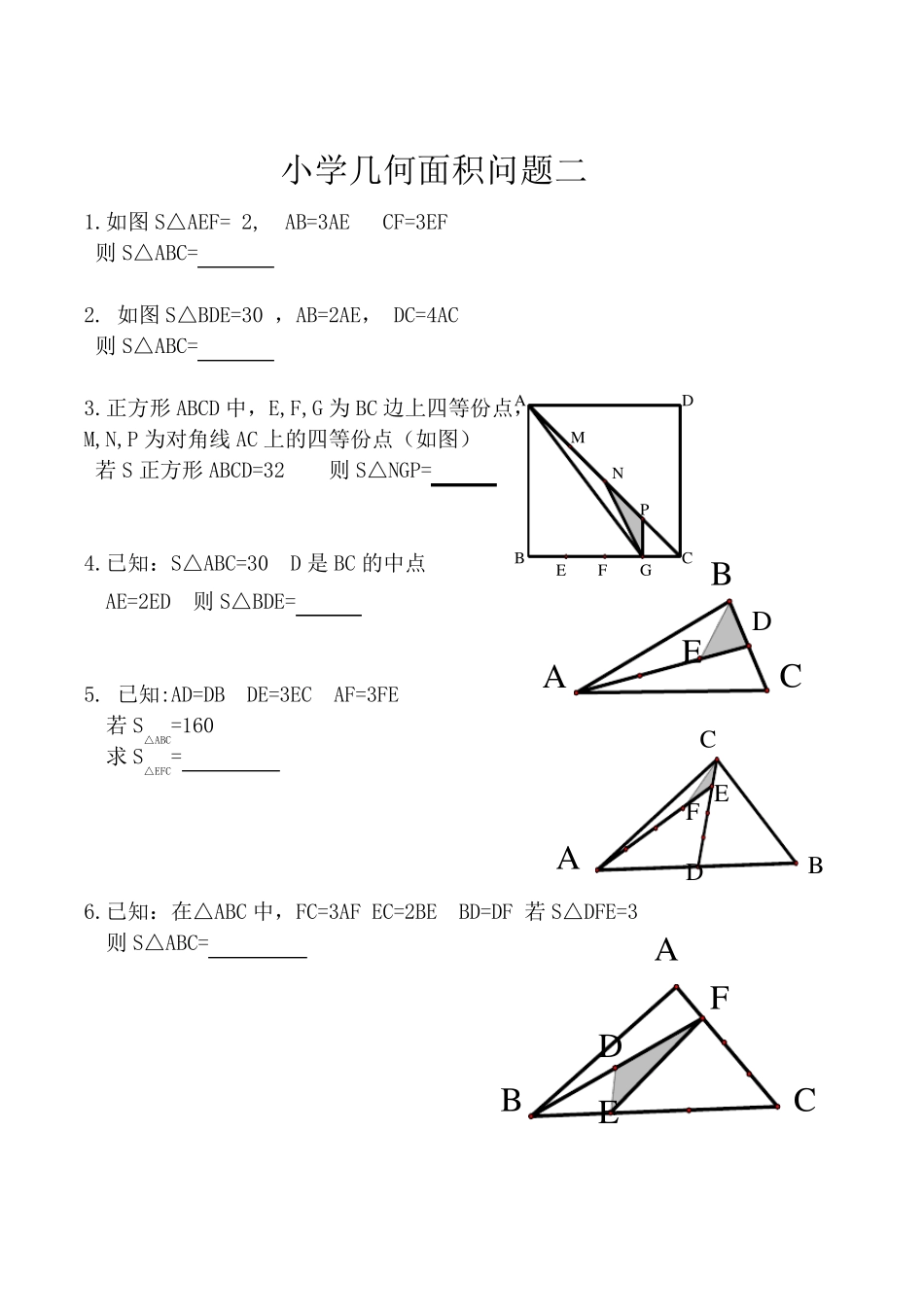
小学几何面积问题一 引理:如图1 在 ABCD 中。P 是AD 上一点,连接PB,PC 则S△PBC=S△ABP+S△pcD= 21 S ABCD 1.已知:四边形 ABCD 为平行四边形,图中的阴影部份面积占平行四边形ABCD 的面积的几分之几? 2. 已知: ABCD 的面积为 18,E 是PC 的中点,求图中的阴影部份面积 3. 在 ABCD 中,CD 的延长线上的一点E,DC=2DE,连接BE 交 AC 于 P 点,(如图)知 S△PDE=1, S△ABP=4,求:平行四边形 ABCD 的面积 4..四边形 ABCD 中,BF=EF=ED,(如图) (1) 若 S 四边形 ABCD =15 则S 阴 = (2)若 S△AEF+ S△BFC=15 则S 四边形 ABCD = (第一题图) A B C D M P N A B C D E P B P A C E D D A C B P 图1 A D C B P A D C B P (适应长方形、正方形) CABE D F A B D C E F G D B A C E F GB F C A E D (3)若S△AEF= 3 S△BFC=2 则 S 四边形 ABCD = 5. 四边形 ABCD 的对角线 BD 被 E,F,G 三点四等份,(如图)若四边形 AECG=15 则 S 四边形 ABCD = 6.四边形 ABCD 的对角线 BD 被 E,F,G 三点四等份,(如图)若阴影部份面积为 15 则 S 四边形 ABCD = 7.若ABCD 为正方形,F 是 DC 的中点,已知:S△BFC= 1 (1)则 S 四边形 ADFB = (2) S△DFE= (3) S△AEB= 8.直角梯形 ABCD 中.AE=ED,BC=18,AD=8,CD=6, 且 BF=2FC,S△GED=S△GFC.求 S 阴= E B C A D F A B C D M N P G F E 小学几何面积问题二 1.如图S△AEF= 2, AB=3AE CF=3EF 则 S△ABC= 2. 如图S△BDE=30 ,AB=2AE, DC=4AC 则 S△ABC= 3.正方形 ABCD 中,E,F,G 为 BC 边上四等份点, M,N,P 为对角线 AC 上的四等份点(如图) 若 S 正方形 ABCD=32 则 S△NGP= 4.已知:S△ABC=30 D 是 BC 的中点 AE=2ED 则 S△BDE= 5. 已知:AD=DB DE=3EC AF=3FE 若 S△ABC=160 求 S△EFC= 6.已知:在△ABC 中,FC=3AF EC=2BE BD=DF 若 S△DFE=3 则 S△ABC= A B C D E B F D C E A B A C E F D DB E CA F 7.ABCD 为平行四边形,AG=GC,BE=EF=FC,若S△GEF=2, 则 S ABCD = 8.ABCD 是梯形,AD // BC(如图) 则 S△AOB= S△AOD= (第 8 题) 9. ABCD 是梯形,AD // BC(如图) 则 S△DOC= S△BOC= (第 9 ...