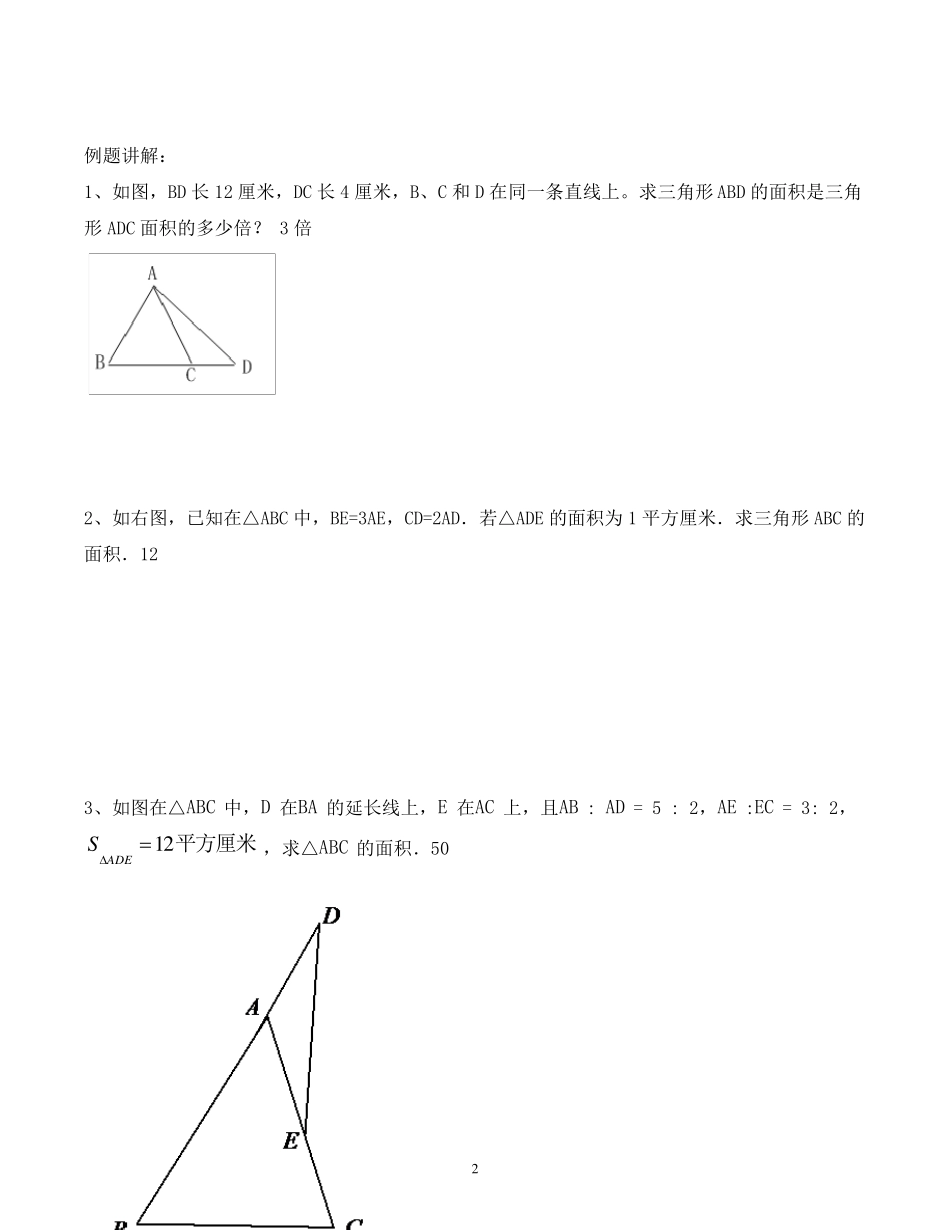
1 教学主题 鸟头定理 教学目标 掌握鸟头定理并会运用 重 要 知识点 1 .鸟头定理 2 . 3 . 易错点 教学过程 鸟头模型 两个三角形中有一个角相等或互补(和为180°),这两个三角形叫做共角三角形。共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在△ABC 中,D,E 分别是AB,AC 上的点如图(或D 、E 分别在BA 、CA 延长线上),则ACABAEADACAEABADSSABCADE (夹角两边:大大小小) 即,共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 2 例题讲解: 1、如图,BD 长12 厘米,DC 长4 厘米,B、C 和D 在同一条直线上。求三角形ABD 的面积是三角形ADC 面积的多少倍? 3 倍 2、如右图,已知在△ABC 中,BE=3AE,CD=2AD.若△ADE 的面积为 1 平方厘米.求三角形ABC 的面积.12 3、如图在△ABC 中,D 在BA 的延长线上,E 在AC 上,且AB : AD = 5 : 2,AE :EC = 3: 2, 平方厘米1 2ADES,求△ABC 的面积.50 3 4.如图,三角形ABC 的面积为3 平方厘米,其中:2:5AB BE ,:3:2BC CD ,三角形BDE 的面积是多少? 2 分之25 5.如图在ABC△中,,D E 分别是,AB AC 上的点,且:2:5AD AB ,:4:7AE AC , 16ADES△平方厘米,求ABC△的面积. 70 6、如图,三角形ABC 中,AB 是AD 的5 倍,AC 是AE 的3 倍,如果三角形ADE 的面积等于 1,那么三角形ABC 的面积是多少? 15 EDCBAEDCBAABECDDCEBA 4 7、如图,三角形 ABC 被分成了甲、乙两部分,4BDDC ,3BE ,6AE ,乙部分面积是甲部分面积的几倍? 5 8.如图,在三角形 ABC 中,D 为 BC 的中点,E 为 AB 上的一点,且13BEAB,已知四边形 EDAC的面积是 35,求三角形 ABC 的面积。42 9、如图所示,在平行四边形 ABCD 中,E 为 AB 的中点,2AFCF,三角形 AFE(图中阴影部分)的面积为 8 平方厘米.平行四边形的面积是多少平方厘米?48 乙甲EDCBAEFDCBA 5 10、已知DEF△的面积为 7 平方厘米,,2,3BECE ADBD CFAF,求ABC△的面积. 24 11、如下图,在三角形 ABC 中,BD=2AD ,AG=2CG ,BE=EF=FC ,求四边形 DGFE 面积占三角形 ABC的几分之几? 9 分之 4 12.如下图,长方形 ABCD 的面积为 90 平方厘米,并且有 AE= 13 EC,CF= 13 BC,求阴影部分三角形 DEF的面积。 30 A D...