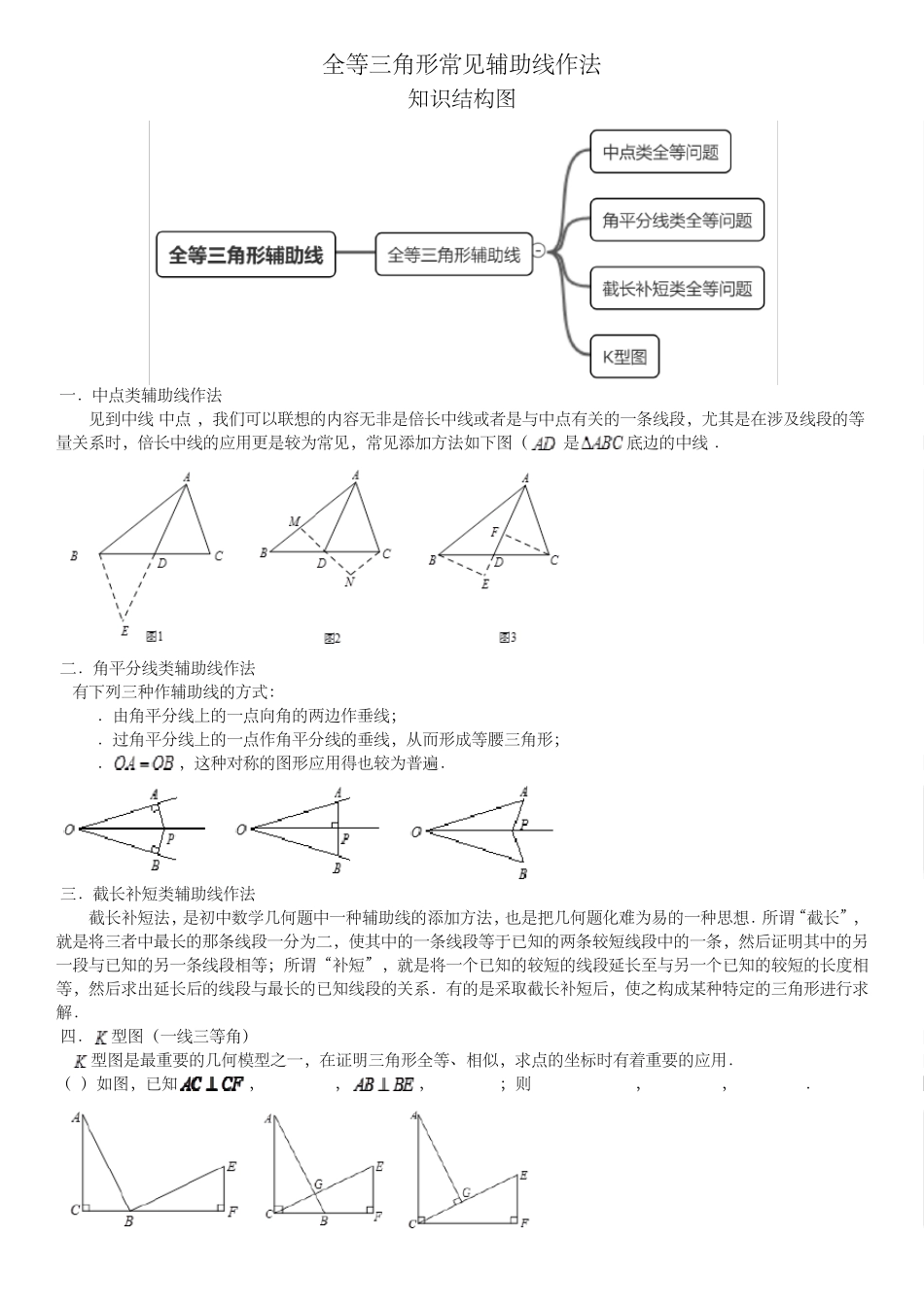
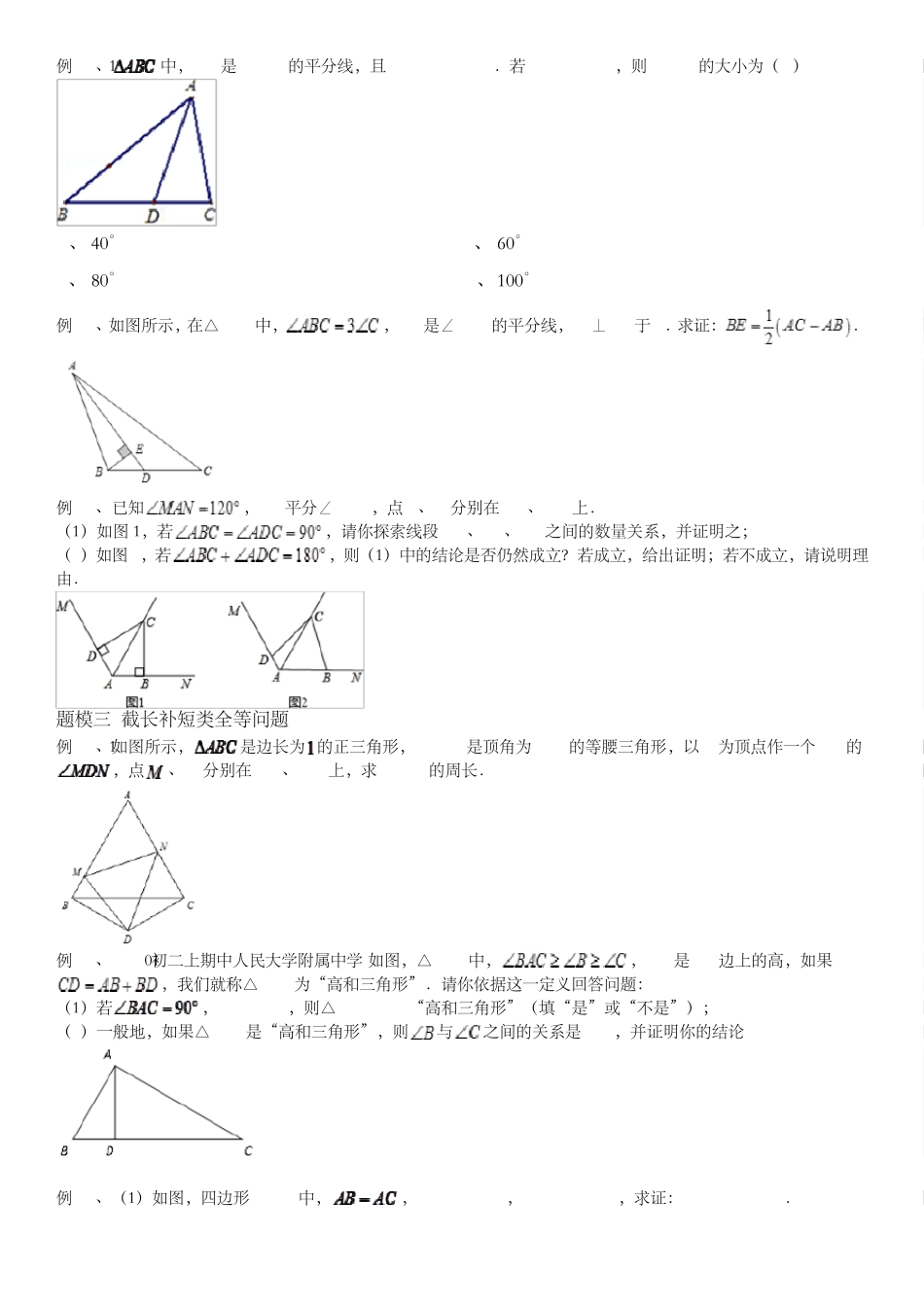
全等三角形常见辅助线作法 知识结构图 一.中点类辅助线作法 见到中线(中点),我们可以联想的内容无非是倍长中线或者是与中点有关的一条线段,尤其是在涉及线段的等量关系时,倍长中线的应用更是较为常见,常见添加方法如下图( 是底边的中线). 二.角平分线类辅助线作法 有下列三种作辅助线的方式: 1.由角平分线上的一点向角的两边作垂线; 2.过角平分线上的一点作角平分线的垂线,从而形成等腰三角形; 3.,这种对称的图形应用得也较为普遍. 三.截长补短类辅助线作法 截长补短法,是初中数学几何题中一种辅助线的添加方法,也是把几何题化难为易的一种思想.所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段等于已知的两条较短线段中的一条,然后证明其中的另一段与已知的另一条线段相等;所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等,然后求出延长后的线段与最长的已知线段的关系.有的是采取截长补短后,使之构成某种特定的三角形进行求解. 四.型图(一线三等角) 型图是最重要的几何模型之一,在证明三角形全等、相似,求点的坐标时有着重要的应用. (1)如图,已知,,,;则,,. (2)型图变化:将向右移动会出现下面两种情况: ①如图,已知,,,,,则,; ②如图,已知,,,,,则,. 题模一 中点类全等问题 例 1.1、如图,已知在中,是边上的中线,是上一点,延长交于,,求证:. 例 1.2、在中,,点为的中点,点、分别为、上的点,且.以线段、、为边能否构成一个三角形?若能,该三角形是锐角三角形、直角三角形或钝角三角形? 例 1.3、八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧. 【探究与发现】 (1)如图 1,AD是△ABC的中线,延长 AD至点 E,使 ED=AD,连接 BE,写出图中全等的两个三角形______ 【理解与应用】 (2)填空:如图 2,EP是△DEF的中线,若 EF=5,DE=3,设 EP=x,则 x的取值范围是______. (3)已知:如图 3,AD是△ABC的中线,∠BAC=∠ACB,点 Q在 BC的延长线上,QC=BC,求证:AQ=2AD. 例 1.4、在△ABC中,D为 BC边的中点,在三角形内部取一点 P,使得.过点 P作 PE⊥AC于点 E,PF⊥AB于点 F. (1)如图 1,当时,判断的 DE与 DF的数量关系,直接写出你的结论; (2)如图 2,当,其它条件不变时,(1)中的结论是否发生改变?请说明理由....