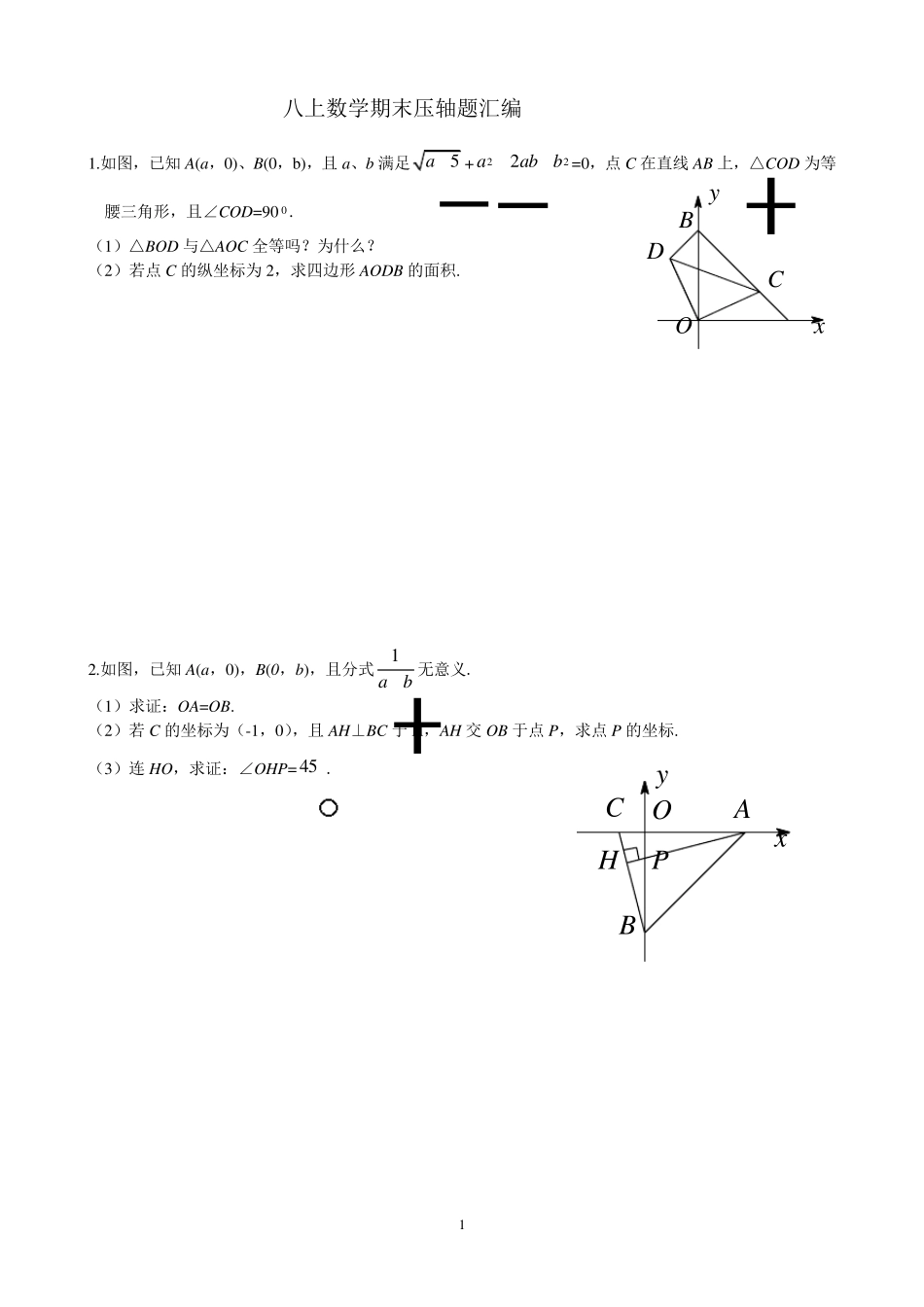
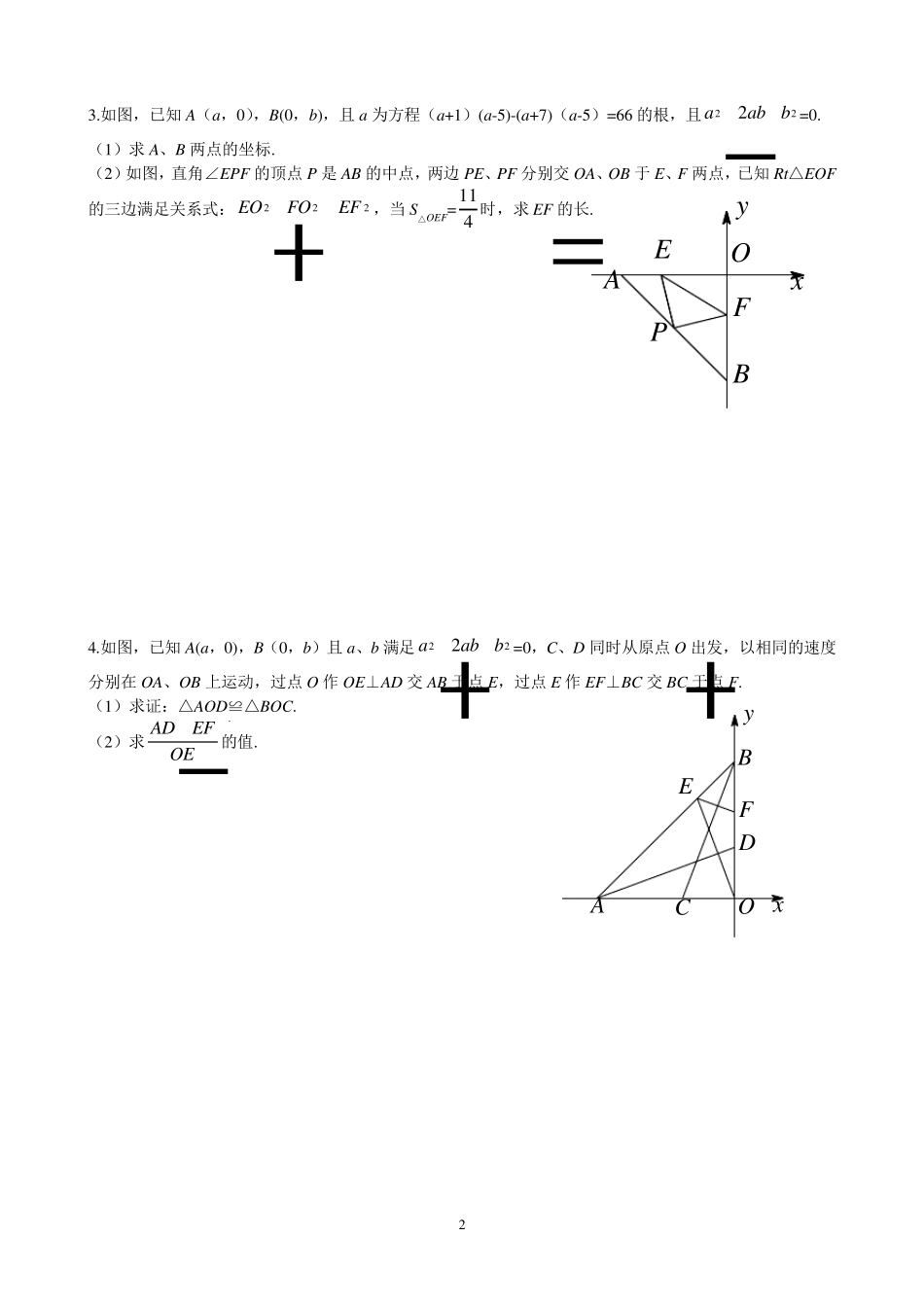
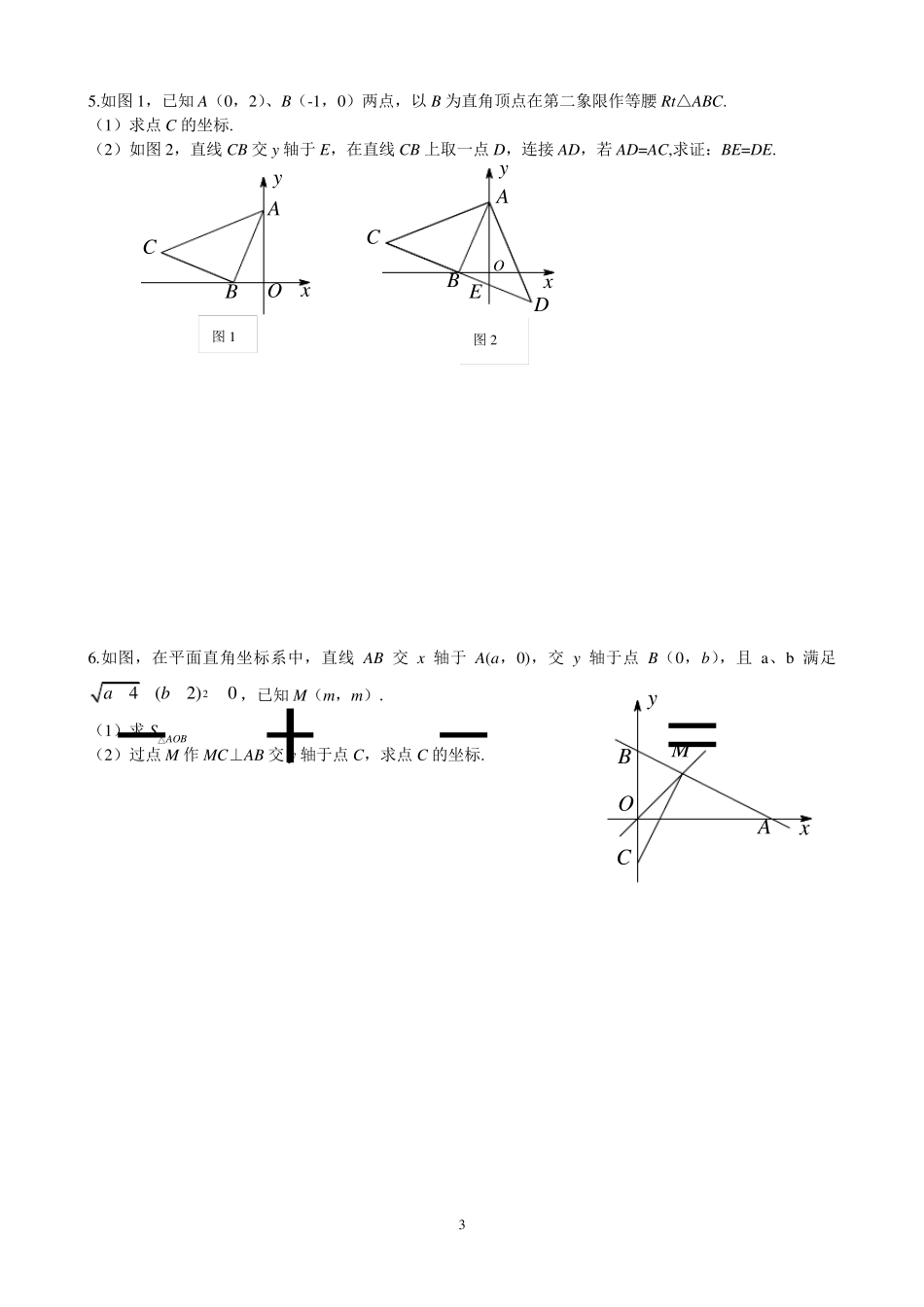
1 八上数学期末压轴题汇编 1.如图,已知A(a,0)、B(0,b),且a、b 满足5a+222aabb =0,点C 在直线AB 上,△COD 为等腰三角形,且∠COD=90 0. (1)△BOD 与△AOC 全等吗?为什么? (2)若点C 的纵坐标为2,求四边形AODB 的面积. 2.如图,已知A(a,0),B(0,b),且分式1ab 无意义. (1)求证:OA=OB. (2)若 C 的坐标为(-1,0),且AH⊥BC 于 H,AH 交 OB 于点P,求点P 的坐标. (3)连 HO,求证:∠OHP=45 . xyCDBOHyxCPABO 2 3.如图,已知A(a,0),B(0,b),且a 为方程(a+1)(a-5)-(a+7)(a-5)=66 的根,且222aabb =0. (1)求A、B 两点的坐标. (2)如图,直角∠EPF 的顶点P 是 AB 的中点,两边 PE、PF 分别交 OA、OB 于 E、F 两点,已知Rt△EOF的三边满足关系式:222EOFOEF ,当 S△OEF= 114 时,求EF 的长. 4.如图,已知A(a,0),B(0,b)且a、b 满足222aabb =0,C、D 同时从原点O 出发,以相同的速度分别在 OA、OB 上运动,过点O 作 OE⊥AD 交 AB 于点E,过点E 作 EF⊥BC 交 BC 于点F. (1)求证:△AOD≌△BOC. (2)求ADEFOE的值. yxOFPABEyxDAOFCEB 3 5.如图1,已知A(0,2)、B(-1,0)两点,以B 为直角顶点在第二象限作等腰Rt△ABC. (1)求点C 的坐标. (2)如图2,直线CB 交y 轴于E,在直线CB 上取一点D,连接AD,若AD=AC,求证:BE=DE. 6.如图,在平面直角坐标系中,直线AB 交x 轴于A(a,0),交y 轴于点B(0,b),且a、b 满足24(2)0ab,已知M(m,m). (1)求S△AOB (2)过点M 作MC⊥AB 交y 轴于点C,求点C 的坐标. xyABCO图1 xyDEABCO图2 xyMACBO 4 7.如图(1),等边三角形△ABC 中,D 为AB 边上的动点,以CD 为一边,向上作等边△EDC,连接AE. (1)△DBC 和△EAC 会全等吗?说明理由; (2)如图(1)求证:AE∥BC. (3)如图(2),(1)中动点D 运动到边BA 的延长线上,仍作等边△EDC,请问是否仍有AE∥BC?证明你的猜想. 8.如图,D 是线段OC 的垂直平分线上的点,AD 平分△AOC 的外角,DF⊥AC 于F. (1)求证:∠ODC=∠OAC; (2)求证:AOACAE=2 (3)求证:AOACOE=2 图1 CDEBACDEBA图2 yxDEACOF 5 (4)变式:如图,若点P 在MAC 的平分线的反向延长线上,若∠OPC=∠OAC,作 PN⊥AO 于 N,现给出两个结论:① AOACAN的值不变;② ACAOAN的值不变.其中有且只有一个结论正确,...