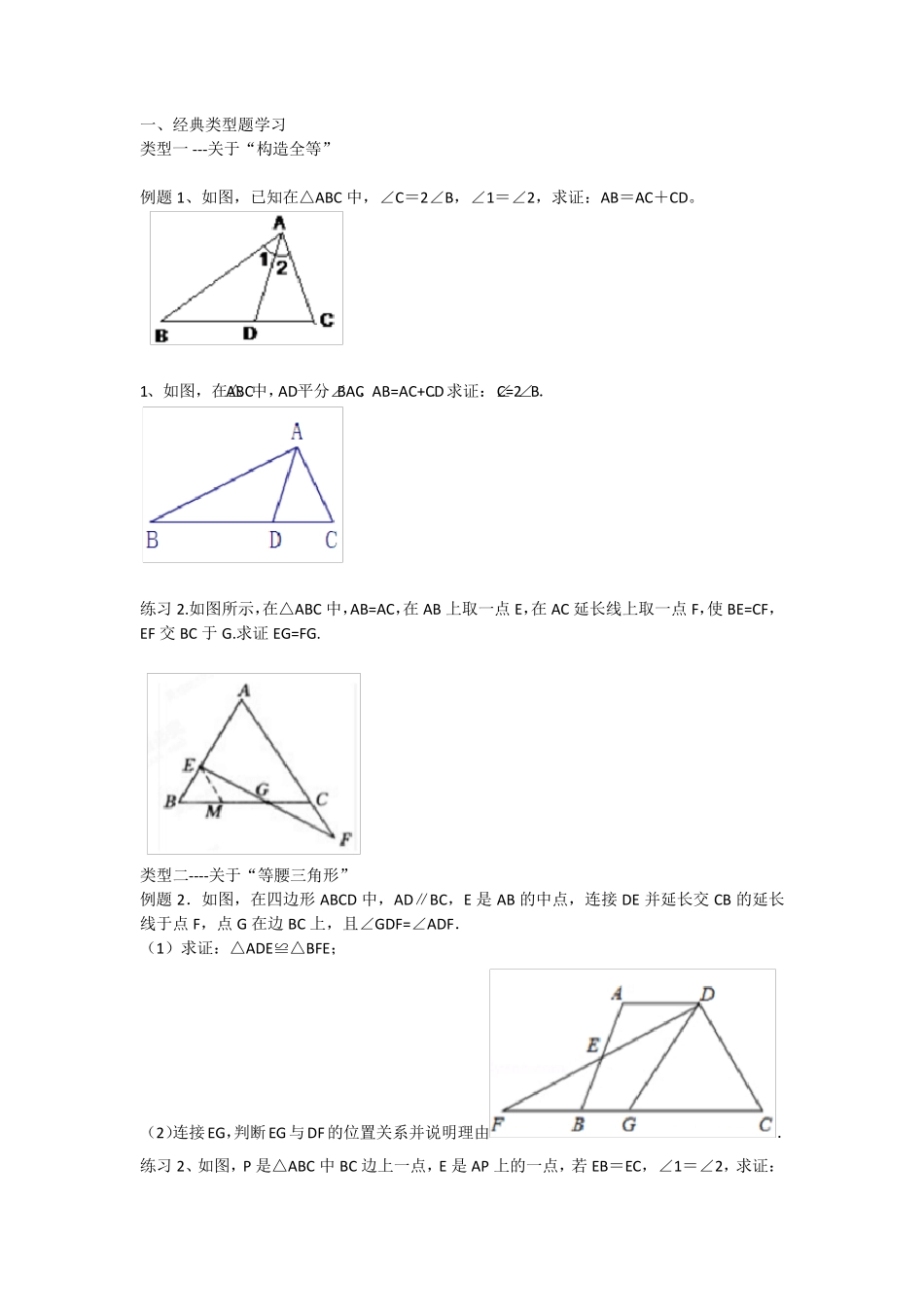
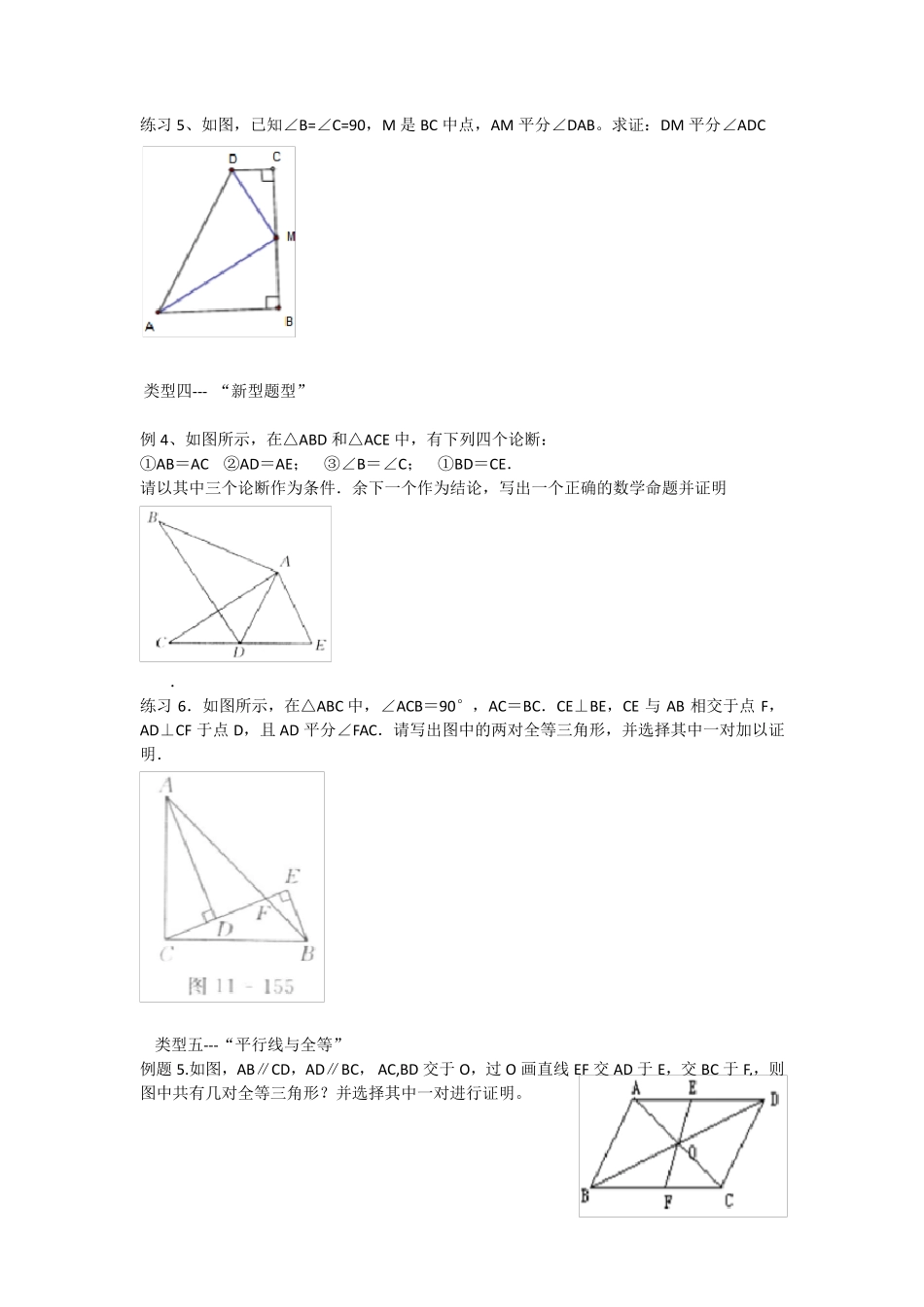
一、经典类型题学习 类型一 ---关于“构造全等” 例题1、如图,已知在△ABC 中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD。 1、如图,在△ABC中,AD平分∠BAC,AB=AC+CD.求证:∠C=2∠B. 练习2.如图所示,在△ABC 中,AB=AC,在 AB 上取一点 E,在 AC 延长线上取一点 F,使 BE=CF,EF 交 BC 于G.求证 EG=FG. 类型二----关于“等腰三角形” 例题2.如图,在四边形 ABCD 中,AD∥BC,E 是 AB 的中点,连接 DE 并延长交 CB 的延长线于点 F,点 G 在边 BC 上,且∠GDF=∠ADF. (1)求证:△ADE≌△BFE; (2)连接EG,判断EG与DF的位置关系并说明理由. 练习2、如图,P是△ABC 中 BC 边上一点,E 是 AP上的一点,若 EB=EC, ∠1=∠2,求证:AP⊥BC。 练习3、如图所示,∠BAC=∠ABD,AC=BD,点O 是AD、BC 的交点,点E 是AB 的中点.试判断OE 和AB 的位置关系,并给出证明. 类型题三---关于“角平分线” 例题3、如图,已知∠MON 的边 OM 上有两点A、B,边 ON 上有两点C、D,且 AB=CD,P为∠MON 的平分线上一点。问: (1)△ABP与△PCD 是否全等?请说明理由。 (2)△ABP与△PCD 的面积是否相等?请说明理由。 练习4、 如图所示,在△ABC 中,AD 平分∠BAC,DG⊥BC 且平分 BC.交BC 于G,DE⊥AB 于 E,DF⊥AC 交AC 的延长线于F. (1)说明BE=CF 的理由; (2)如果 AB=8,AC=6,求 AE、BE 的长. 练习5、如图,已知∠B=∠C=90,M 是BC 中点,AM 平分∠DAB。求证:DM 平分∠ADC 类型四--- “新型题型” 例4、如图所示,在△ABD 和△ACE 中,有下列四个论断: ①AB=AC ②AD=AE; ③∠B=∠C; ①BD=CE. 请以其中三个论断作为条件.余下一个作为结论,写出一个正确的数学命题并证明 . 练习6.如图所示,在△ABC 中,∠ACB=90°,AC=BC.CE⊥BE,CE 与 AB 相交于点F,AD⊥CF 于点D,且 AD 平分∠FAC.请写出图中的两对全等三角形,并选择其中一对加以证明. 类型五---“平行线与全等” 例题5.如图,AB∥CD,AD∥BC, AC,BD 交于 O,过 O画直线 EF 交 AD 于 E,交 BC 于 F,,则图中共有几对全等三角形?并选择其中一对进行证明。 5.如图,AB∥CD,AD∥BC,E 是CA 延长线上的点,F 是AC 延长线上的点,且AE=CF,求证:∠E=∠F 三、跟踪训练: 1 如图,在△ABC 中,AB=AC,BD 平分∠ABC,DE⊥BD 于D,交BC...