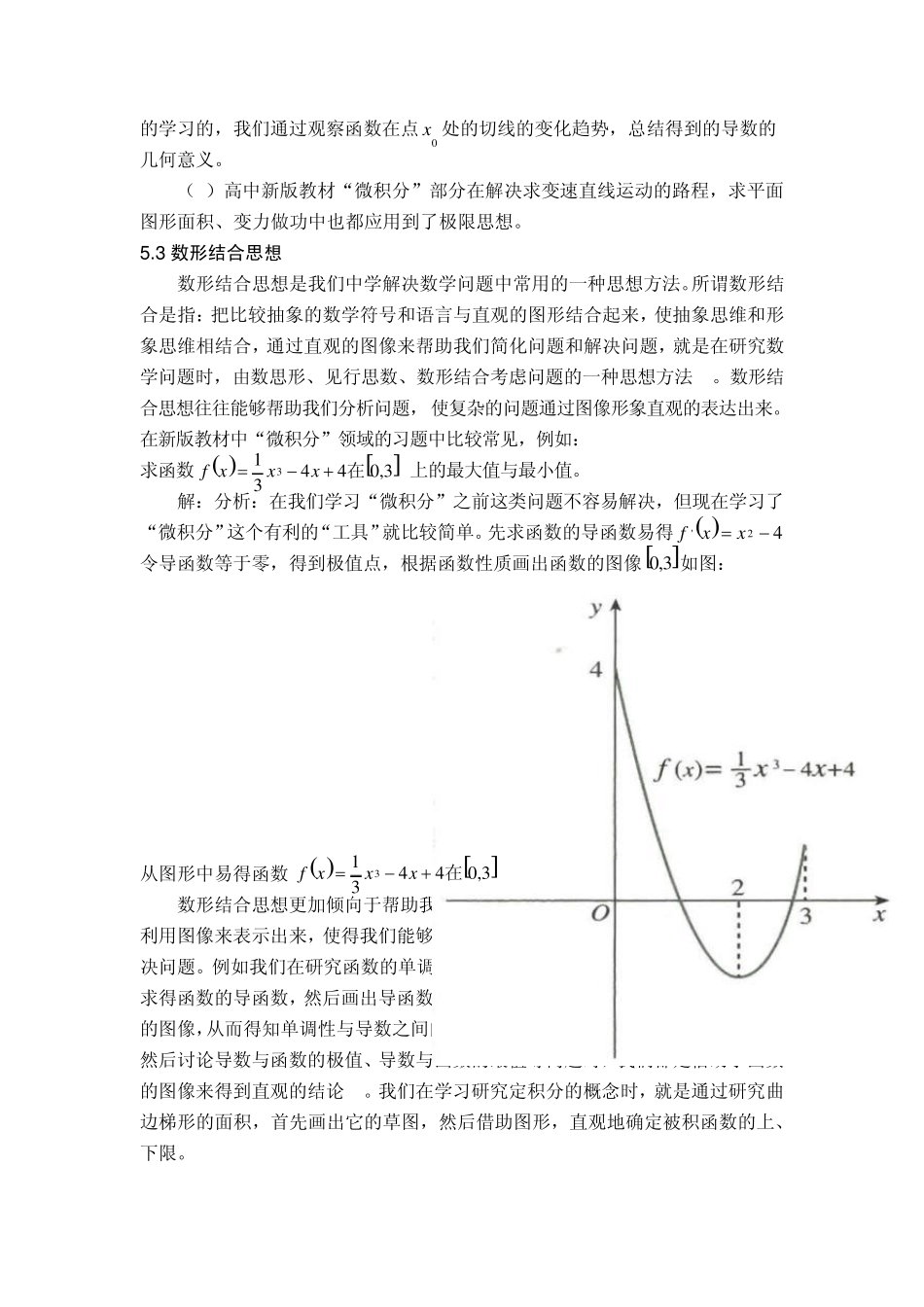
数学思想方法的解释有多种多样,其中胡炯涛《数学教学论》广西教育出版社,一书中指出数学思想方法则是数学知识发生过程中的提炼、抽象、概括和升华,是对数学规律更一般的认识,它蕴藏在数学知识之中,需要学习者去挖掘[6]。数学思想方法分为两部分,一是数学思想,二是数学方法,其中数学思想是指我们对教材中理论知识及内容最本质的认识,而数学方法是数学思想的具体化形式,运用到实际的题目中[20]。下面就具体来阐述一下微积分习题中的数学思想方法: 5 .1 函数思想 函数思想是我们在中学阶段中常见的一种思想方法,是指用函数的概念、性质、特点去分析问题、转化问题和解决问题的一种思维,函数思想是一个基本的数学思想,方程,不等式问题可以在函数的观点下统一起来,数列是特殊的函数,集合论的知识作为建立函数的基础,也包括在其中[11]。在新版教材微积分的内容中,函数思想更为重要,其中一部分题目就是借助“微积分”这个工具,最后还是依据函数的基本性质去解决问题。例如: 一条长为 l 的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,两段铁丝的长度分别是多少?[12](新版教材人教 A版选修2–2课本 37页习题) 解:设其中一段铁丝的长度为 x ,则另一段为xl ,面积为 s 根据题意得: 整理得: 求导数,并令导数等于零,解得: 分析:这类题型在新版教材中为常见的一种题型,根据题意得到函数表达式,借助“微积分”这个工具,结合函数的性质来解决问题。当 时导函数的函数值为零,这时函数取得最小值(函数的性质)。 例如:有一家宾馆有 50个房间共旅客居住,当每个房间定价为每天 180元时,房间会全部住满;房间单价每增加 10元,就会有一个房间空闲,如果旅客居住房间,宾馆每间每天需花费 20元的各种维护费用,房间定价多少时,宾馆利润最大? 分析:这是一个生活中实际的问题,解决方法,根据题意列出函数表达式,我们4444xlxlxxs162222llxxs2lx 2lx 要找到关键问题,利润是由房间数乘以房间定价让后减去房间数乘以房间维护费,所以关键就是房间数,我们设房间定价为x 元,利润为s , 则 对x 进行求导,并令导数为零,得到350x,即可解得利润的最大值 把数学问题用函数表示出来,借助“微积分工具”去解决数学问题,这是我们常用的方法,即函数思想结合“微积分”去解决问题。特别的我们在学习了“微积分”之后,这种题型是我们常见题型及常...