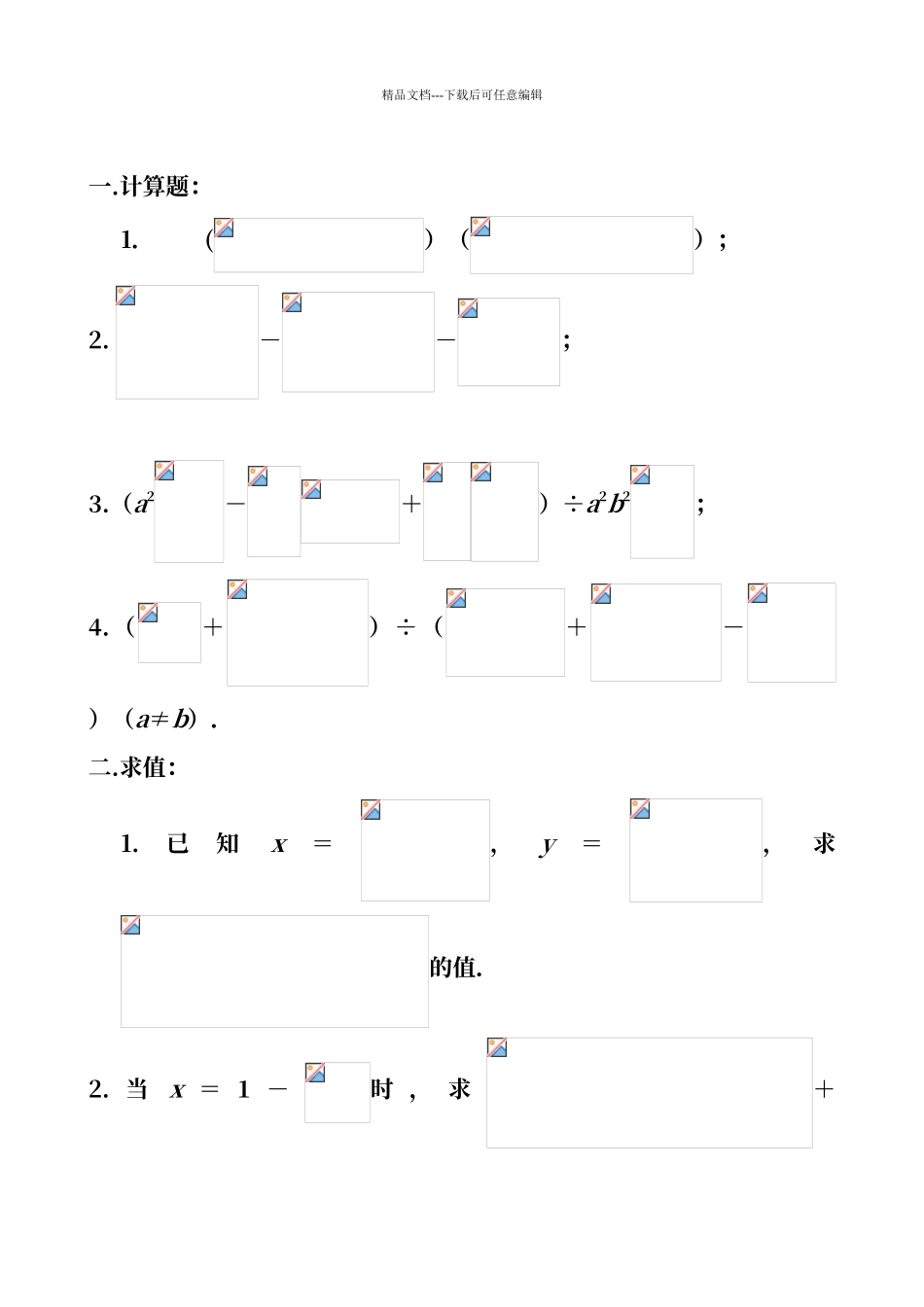
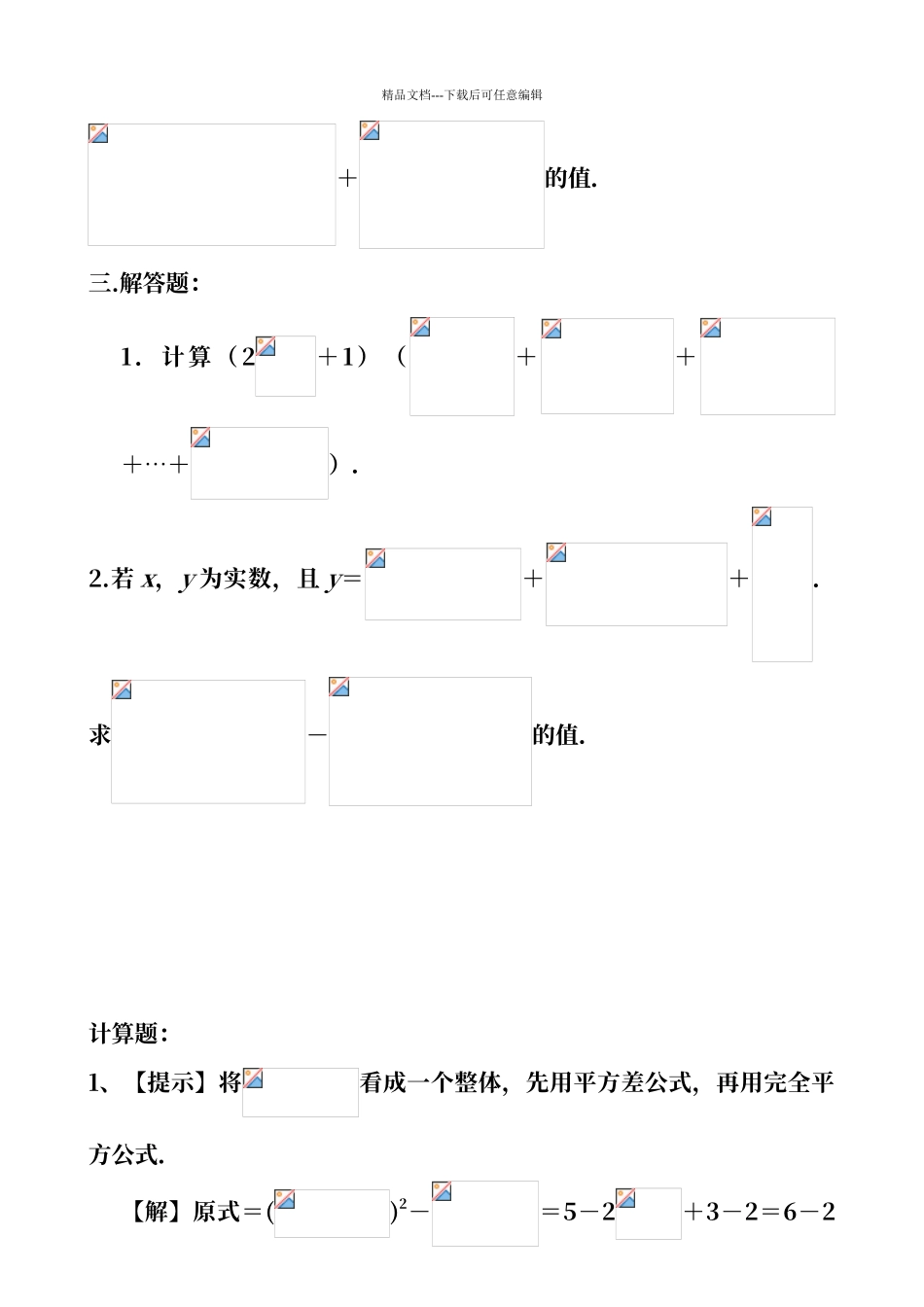
精品文档---下载后可任意编辑 一.计算题:1.()();2. --;3.(a2-+)÷a2b2;4.(+)÷(+-)(a≠b).二.求值:1.已知x=,y=,求的值.2. 当x = 1 -时 , 求+精品文档---下载后可任意编辑+的值.三.解答题:1.计算( 2+1)(+++…+).2.若 x,y 为实数,且 y=++.求-的值.计算题:1、【提示】将看成一个整体,先用平方差公式,再用完全平方公式.【解】原式=()2-=5-2+3-2=6-2精品文档---下载后可任意编辑.2、【提示】先分别分母有理化,再合并同类二次根式.【 解 】 原 式 =--= 4 +---3+=1.3、【提示】先将除法转化为乘法,再用乘法分配律展开,最后合并同类二次根式.【解】原式=(a2-+)·=-+=-+=.4、【提示】本题应先将两个括号内的分式分别通分,然后分解因式并约分.【解】原式=÷精品文档---下载后可任意编辑=÷=·=-.【点评】本题假如先分母有理化,那么计算较烦琐.求值:1.、【提示】先将已知条件化简,再将分式化简最后将已知条件代入求值.【 解 】 ∵ x === 5 + 2,y===5-2.∴ x+y=10,x-y=4,xy=52-(2)2=1.精品文档---下载后可任意编辑====.【点评】本题将 x、y 化简后,根据解题的需要,先分别求出“x+y”、“x-y”、“xy”.从而使求值的过程更简捷.2、【提示】注意:x2+a2=,∴ x2 + a2 - x=(- x ) , x2 - x= - x (-x).【解】原式=-+精品文档---下载后可任意编辑=====.当 x=1-时,原式==-1-.【点评】本题假如将前两个“分式”分拆成两个“分式”之差,那么化简会更简 便 . 即 原 式 =-+精品文档---下载后可任意编辑=-+=.解答题:1、【提示】先将每个部分分母有理化后,再计算.【 解 】 原 式 = ( 2+ 1 ) (+++…+)=(2+1)[()+()+()+…+()]=(2+1)()=9(2+1).【点评】本题第二个括号内有 99 个不同分母,不可能通分.这里采纳的是先分母有理化,将分母化为整数,从而使每一项转化成两数之差精品文档---下载后可任意编辑然后逐项相消.这种方法也叫做裂项相消法.2、【提示】要使 y 有意义,必须满足什么条件你能求出 x,y 的值吗【解】要使 y 有意义,必须,即∴ x=.当 x= 时,y= .又 ∵ -=-=||-||∵ x=,y=精品文档---下载后可任意编辑,∴ <.∴ 原 式 =-= 2当 x =,y=时,原式=2=.【点评】解本题的关键是利用二次根式的意义求出 x 的值,进而求出 y 的值.