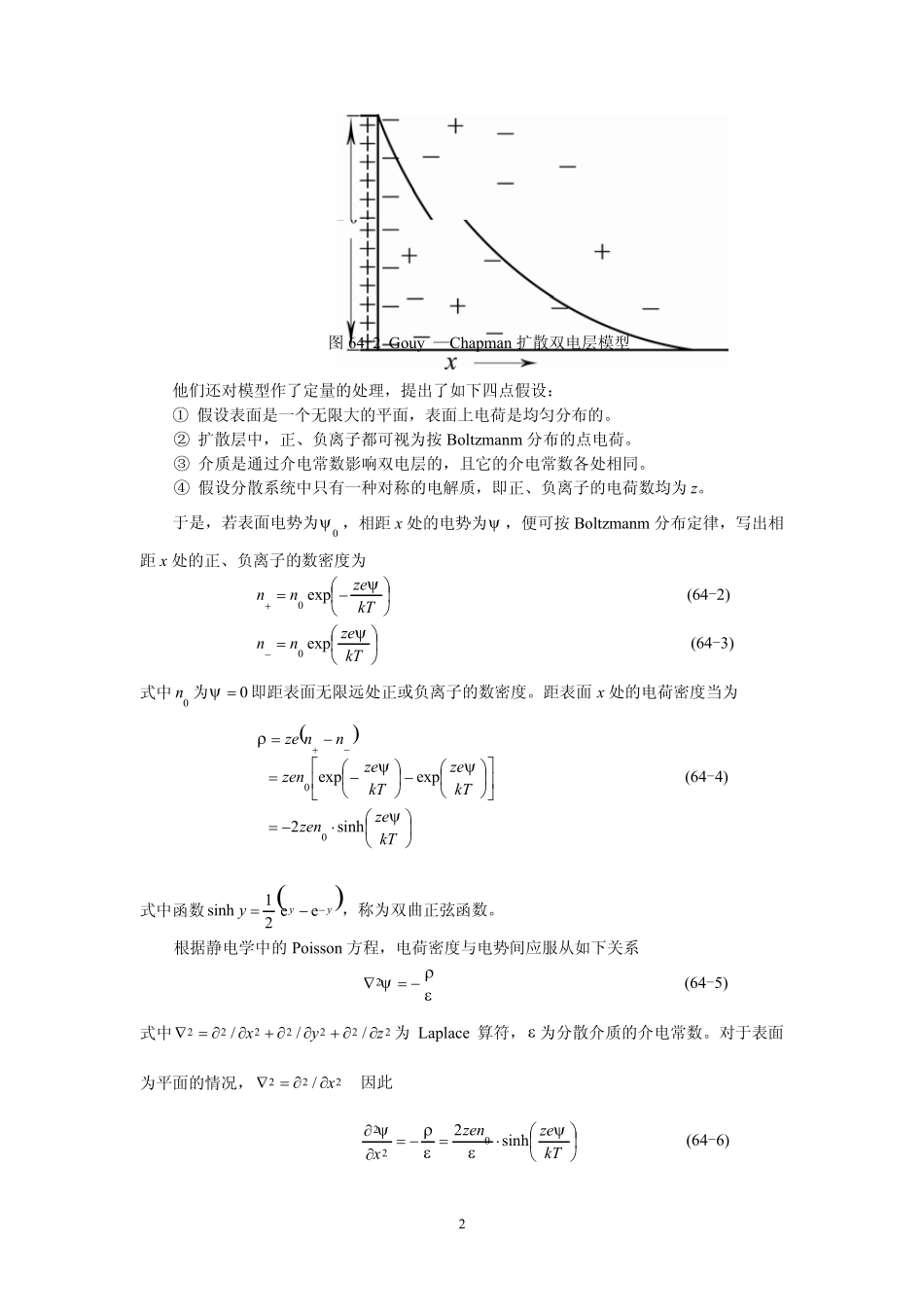
164 扩散双电层理论和Zeta 电势 胶体粒子的表面常因解离、吸附、极化、摩擦等原因而带电,分散介质则带反电荷,因此,在相界面上便形成了双电层。胶体的这种结构决定了它的电学性质,并对其稳定性起着十分重要的作用。本专题便来讨论胶体的双电层结构,并从中引出一个决定胶体电学性质和稳定性的重要指标—— ς (Zeta)电势。 1.双电层模型 (1) Helmholtz模型 1879 年,Helmholtz 在研究胶体在电场作用下运动时,最早提出了一个双电层模型。这个模型如同一个平板电容器,认为固体表面带有某种电荷,介质带有另一种电荷,两者平行,且相距很近,就像图 64-1 所示。 图 64-1 Helmholtz 双电层模型 按照这个模型,若固体表面的电势为0ψ ,正、负电荷的间距为δ ,则双电层中的电势随间距直线下降,且表面电荷密度σ 与电势0ψ 的关系如下式表示 δεψσ0= (64-1) 式中ε为介质的介电常数。 显然,这是一个初级双电层模型,它只考虑到带电固体表面对介质中反离子的静电作用,而忽视了反离子的热运动。虽然,它对胶体的早期研究起过一定的作用,但无法准确地描述胶体在电场作用下的运动。 (2) Gouy(古依)—Chapman (恰普曼)模型 由于 Helmholtz 模型的不足,1910 和1913 年,Gouy 和Chapman 先后作出改进,提出了一个扩散双电层模型。这个模型认为,介质中的反离子不仅受固体表面离子的静电吸引力,从而使其整齐地排列在表面附近,而且还要受热运动的影响,使其离开表面,无规则地分散在介质中。这便形成如图 64-2 所示的扩散双电层结构。 2 图64-2 Gouy —Chapman 扩散双电层模型 他们还对模型作了定量的处理,提出了如下四点假设: ① 假设表面是一个无限大的平面,表面上电荷是均匀分布的。 ② 扩散层中,正、负离子都可视为按 Boltzmanm 分布的点电荷。 ③ 介质是通过介电常数影响双电层的,且它的介电常数各处相同。 ④ 假设分散系统中只有一种对称的电解质,即正、负离子的电荷数均为 z。 于是,若表面电势为0ψ ,相距 x 处的电势为ψ ,便可按 Boltzmanm 分布定律,写出相距 x 处的正、负离子的数密度为 ⎟⎠⎞⎜⎝⎛−=+kTzennψexp0 (64-2) ⎟⎠⎞⎜⎝⎛=−kTzennψexp0 (64-3) 式中0n 为0=ψ即距表面无限远处正或负离子的数密度。距表面 x 处的电荷密度当为 ()⎟⎠⎞⎜⎝⎛⋅−=⎥⎦⎤⎢⎣⎡⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛−=−=−+kTzezenkTzekTzezennnzeψψψ...