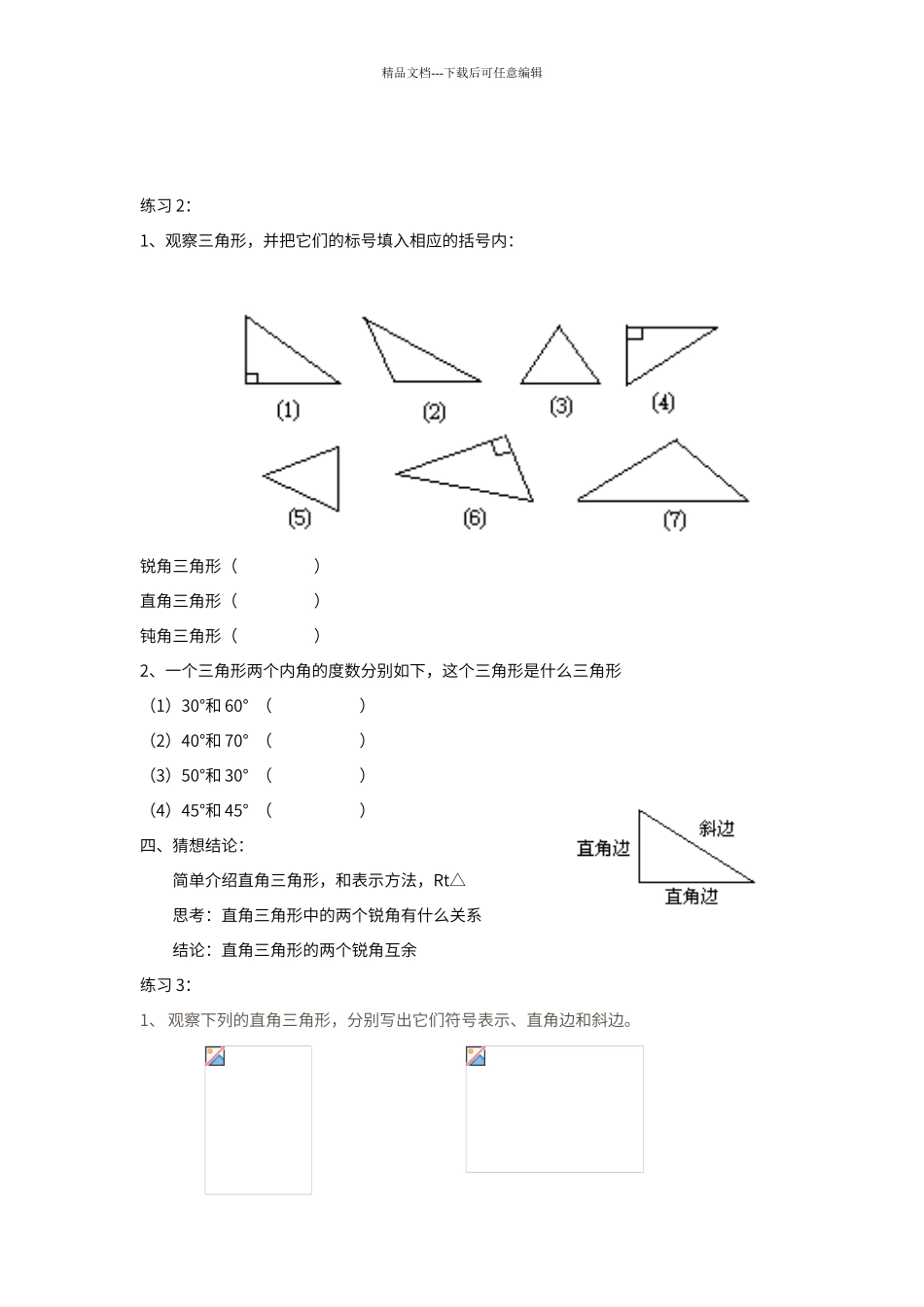
精品文档---下载后可任意编辑三角形1.认识三角形1、它的三个顶点分别是 ,三条边分别是 ,三个内角分别是 。2、分别量出这三角形三边的长度,并计算任意两边之和以及任意两边之差。你发现了什么结论:三角形任意两边之和大于第三边三角形任意两边之差小于第三边例:有两根长度分别为 5cm 和 8cm 的木棒,用长度为 2cm 的木棒与它们能摆成三角形吗为什么长度为 13cm 的木棒呢长度为 7cm 的木棒呢二、巩固练习:1、下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗为什么(单位:cm)(1) 1, 3, 3(2) 3, 4, 7(3) 5, 9, 13(4) 11, 12, 22(5) 14, 15, 302、已知一个三角形的两边长分别是 3cm 和 4cm,则第三边长 X 的取值范围是 。若 X 是奇数,则 X 的值是 。这样的三角形有 个;若 X 是偶数,则 X 的值是 ,这样的三角形又有 个3、一个等腰三角形的一边是 2cm,另一边是 9cm ,则这个三角形的周长是 cm夯实基础1、填空:(1)当 0°<<90°时,是 角;(2)当= °时,是直角;(3)当 90°<<180°时,是 角;(4)当= °时,是平角。2、如右图, AB∥CE,(已知)精品文档---下载后可任意编辑∴∠A= ,( )∴∠B= ,( ) (第 2 题)二、探究练习: 根据知道三角形的三个内角和等于 180°,那么是否对其他的三角形也有这样的一个结论呢(提出问题,激发学生的兴趣)结论:三角形三个内角和等于 180°(几何表示)练习 1:1、推断:(1)一个三角形的三个内角可以都小于 60°; ( )(2)一个三角形最多只能有一个内角是钝角或直角; ( )2、在△ABC 中,(1)∠C=70°,∠A=50°,则∠B= 度;(2)∠B=100°,∠A=∠C,则∠C= 度;(3)2∠A=∠B+∠C,则∠A= 度。3、如右图,在△ABC 中,∠A=°∠=°∠=°求三个内角的度数。解: ∠A+∠B+∠C=180°,( ) ∴ ∴= ∴=从而,∠A= ,∠B= ,∠C= 三、 探究沟通 (第 3 题)练习 1:一个三角形中三个内角可以是什么角(提醒:一个三角形中能否有两个直角钝角呢)★ 按三角形内角的大小把三角形分为三类 锐角三角形 (acute trangle)三个内角都是锐角 直角三角形 (right triangle)有一个内角是直角 钝角三角形(obtuse triangle)有一个内角是钝角精品文档---下载后可任意编辑练习 2:1、观察三角形,并把它们的标号填入相应的括号内:锐角三角形(...