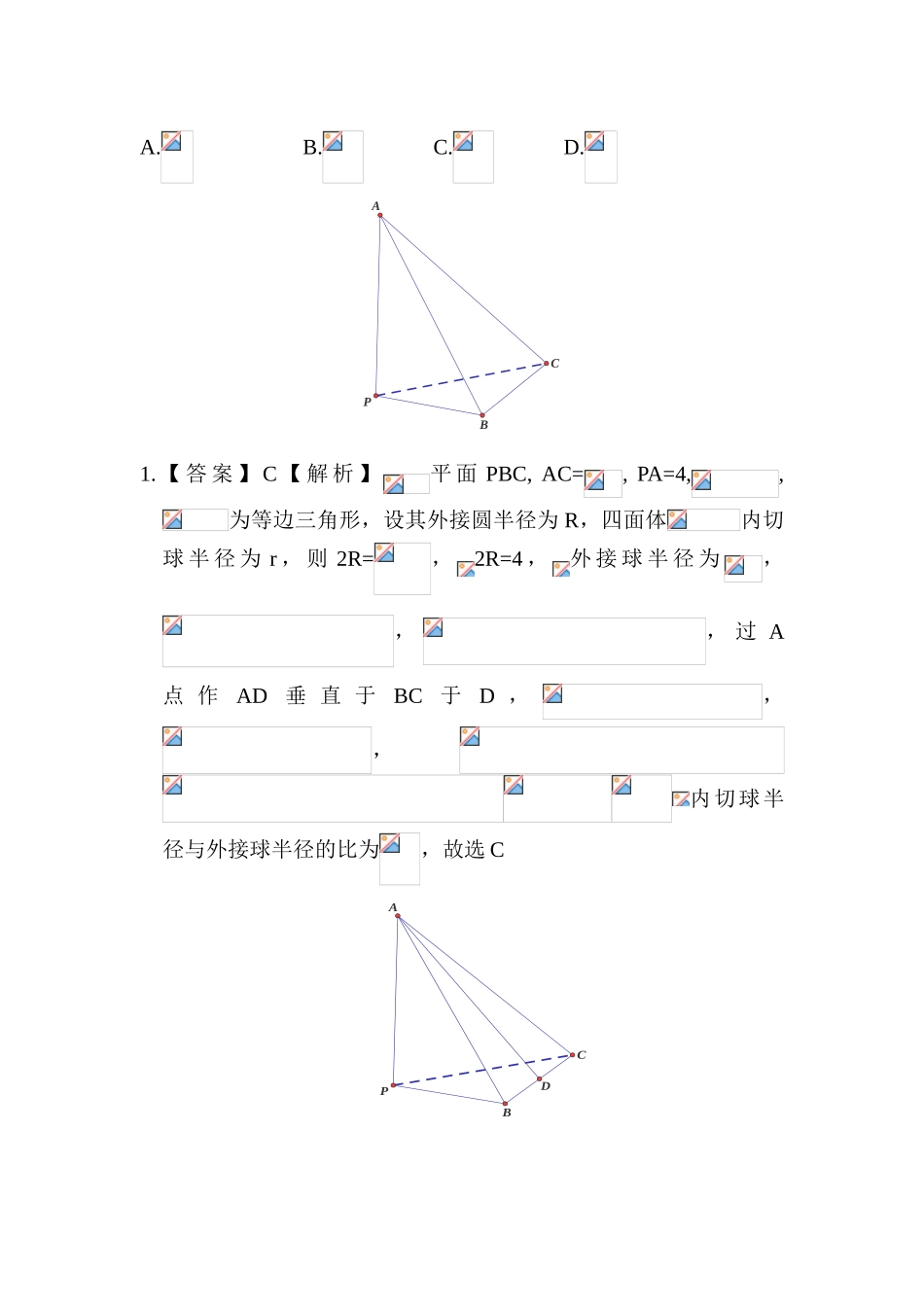
1. 已 知是 等 差 数 列 , 且, 则的 前 8 项 和 为 ( )A.40B.20C.10D.8 1. 【 答 案 】 B 【 解 析 】 由可 得, 即,因此,的前 8 项和为. 2.已知 i 是虚数单位,,则 ( )A.B. C.D.2.【答案】C【解析】由可得,故. 3.已知角是第二象限角,且,且的图像有关直线对称,则 .3.【答案】【解析】由条件可得,则,,由有 关 直 线对 称 可 得,则. 1.(理)已知四面体中, PA=4,AC=,PB= BC=,平面 PBC,则四面体的内切球半径与外接球半径的比( )A.B.C.D.APCB1. 【 答 案 】 C 【 解 析 】平 面 PBC, AC=, PA=4,,为等边三角形,设其外接圆半径为 R,四面体内切球 半 径 为 r , 则 2R=,2R=4 ,外 接 球 半 径 为,,, 过 A点 作AD 垂 直 于BC于D ,,,内切球半径与外接球半径的比为,故选 CAPCBD 2. 已 知 四 面 体中 , PA=4 , AC=,PB= BC=,平 面PBC,则四面体外接球体积为( )A.B.C.D. 2.【答案】 C 【解析】平面 PBC, AC=, PA=4,,为等边三角形,设其外接球半径为 R,,则 2R=,2R=4 ,外 接 球 半 径 为, 其 外 接 球 的 体 积 为 3.若椭圆:和椭圆共长轴,且,给出下列四个命题对的的是 .① 设椭圆的离心率为 e,则;②;③④ 椭圆的焦点为椭圆上的任意一点,椭圆的焦点,为椭圆上的任意一点,则当都取最大角时,⑤ 两椭圆中,椭圆的最短的焦半径比椭圆的最短的焦半径长;3.【答案】②④⑤【解析】由于两椭圆共长轴,因此,又由于,因此,故①错.由于长轴相等,因此成 立 , ② 对 的 . 对 于 ③ 由 于, 因 此,因此③错误.点在椭圆短轴顶点时,张角最大.由于两椭圆长轴相似,因此谁焦距长谁张角大,因此④对的.椭圆的最短的焦半径长为最短的焦半径,因此⑤对的. 1.已知函数,将函数图象上所有点的横坐标缩短为本来的倍(纵坐不变),得到函数的图象,则有关有下列命题,其中真命题的个数是 ( )① 函数是奇函数;② 函数不是周期函数;③ 函数的图像有关点(π,0)中心对称;④ 函数的最大值为.A.1B.2C.3D.41.【答案】A【解析】,① 错误,是偶函数;②错误,即为的一种周期;③ 对的,可以验证恒成立,故(π,0)是的图像的一种对称中心;④ 错误,令 t=cos,t[∈ -1,1],则 m(t)=2t (1-t2)=2( t-t3),令 m′(t)=2( 1-3t2)=0,得.当 t=±1 时,函数值为 0;当时,函数值为;当时...