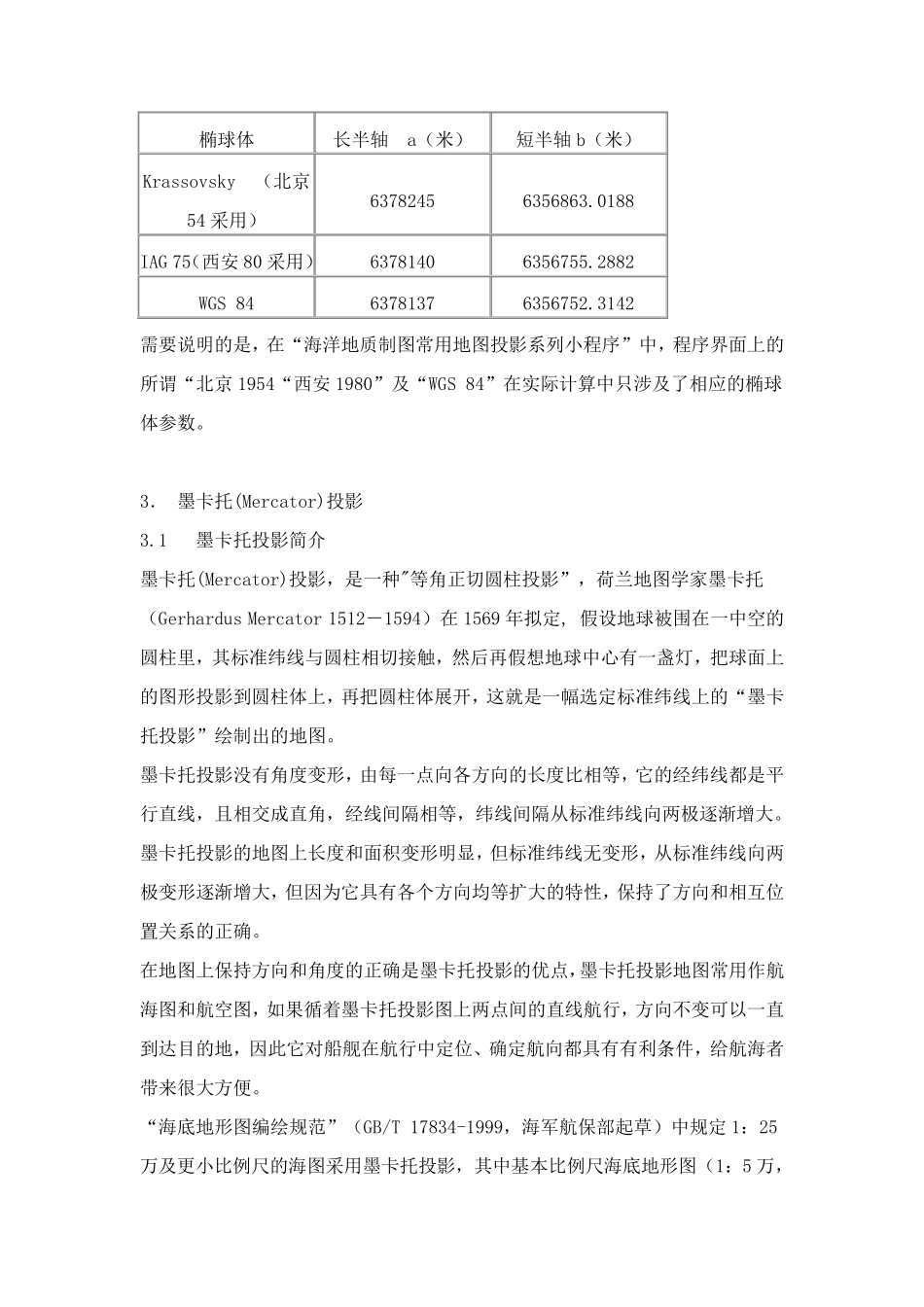
投影计算公式往往表达方式不止一种,有时很难分辨谁对谁错,我只把“墨卡托投影”、“高斯-克吕格投影”、“UTM 投影”、“兰勃特等角投影” (1:100万地形图规范中称作正轴等角圆锥投影,GB/T 14512-93)的正反转换公式列出,因为我基本能保证这些公式的正确性。 “海洋地质制图常用地图投影系列小程序已升级,原下载者请注意下载更新版本。 1. 约定 本文中所列的转换公式都基于椭球体 a -- 椭球体长半轴 b -- 椭球体短半轴 f -- 扁率 e -- 第一偏心率 e’ -- 第二偏心率 N -- 卯酉圈曲率半径 R -- 子午圈曲率半径 B -- 纬度,L -- 经度,单位弧度(RAD) -- 纵直角坐标, -- 横直角坐标,单位米(M) 2. 椭球体参数 我国常用的3 个椭球体参数如下(源自“全球定位系统测量规范 GB/T 18314-2001”): 椭球体 长半轴 a(米) 短半轴b(米) Krassovsky (北京54 采用) 6378245 6356863.0188 IAG 75(西安80 采用) 6378140 6356755.2882 WGS 84 6378137 6356752.3142 需要说明的是,在“海洋地质制图常用地图投影系列小程序”中,程序界面上的所谓“北京1954“西安1980”及“WGS 84”在实际计算中只涉及了相应的椭球体参数。 3. 墨卡托(Mercator)投影 3.1 墨卡托投影简介 墨卡托(Mercator)投影,是一种"等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569 年拟定, 假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。 墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关 系的正确 。 在地图上保持方向和角度的正确 是墨卡托投影的优 点,墨卡托投影地图常用作 航海图和航 空图,如 果 循 着 墨卡托投影图上两点间的直线航 行,方向不 变可 以 一直到达 目 的地,因此 它对 船 舰 在航 行中定位、 确 定航 向都具有有利 条 件 ,给 航 海者带 来 很 大方便 。 “海底 地形图编 绘规 范 ”(GB/T 17...