支持向量机原理

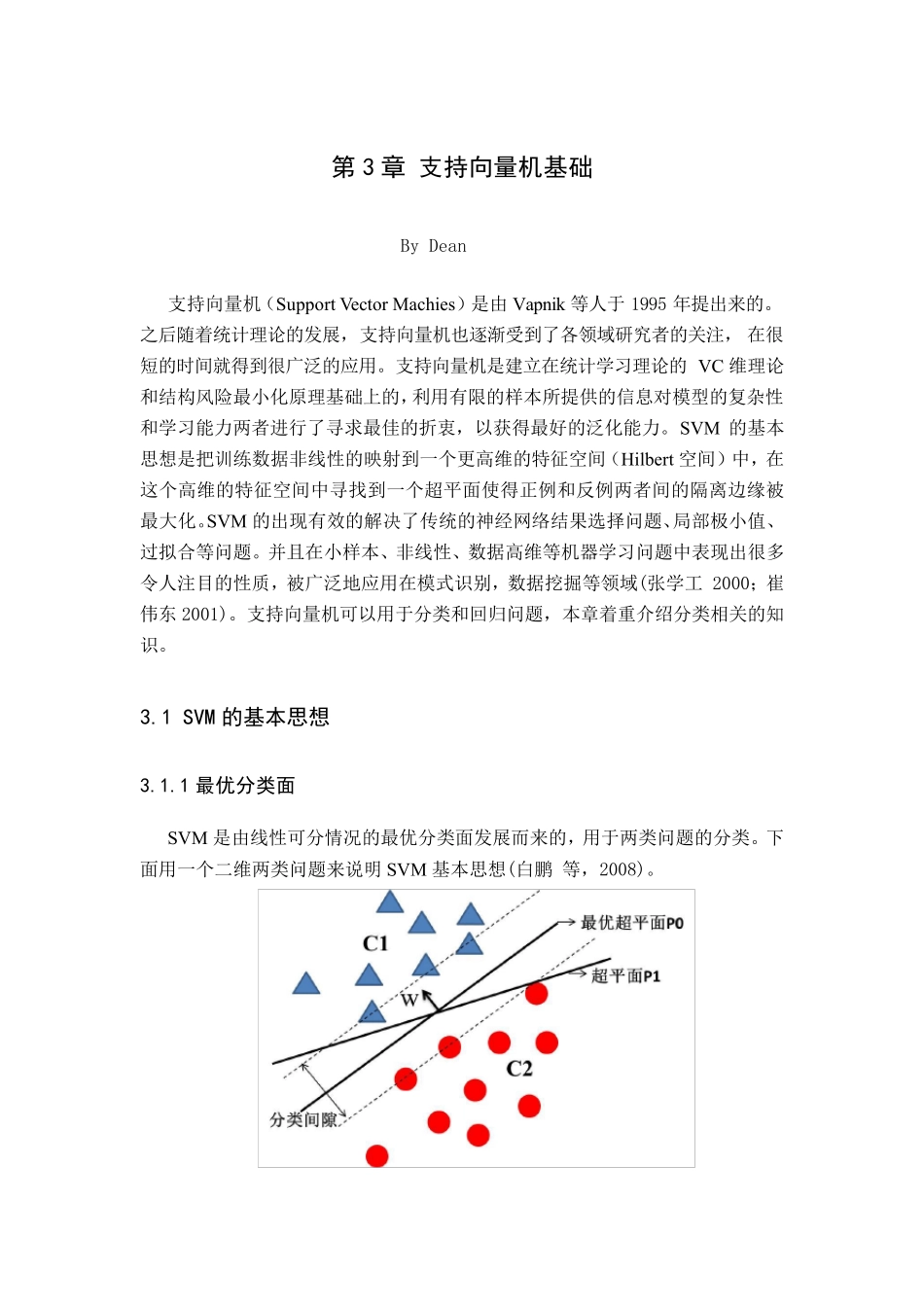
第3 章 支持向量机基础 By Dean 支 持 向 量 机 （ Su pport Vector Machies） 是 由 Vapnik 等 人 于 1995 年 提 出 来 的 。之 后 随 着 统 计 理 论 的 发 展 ， 支 持 向 量 机 也 逐 渐 受 到 了 各 领 域 研 究 者 的 关 注 ， 在 很短 的 时 间 就 得 到 很 广 泛 的 应 用 。 支 持 向 量 机 是 建 立 在 统 计 学 习 理 论 的VC 维 理 论和 结 构 风 险 最 小 化 原 理 基 础 上 的 ，利 用 有 限 的 样 本 所 提 供 的 信 息 对 模 型 的 复 杂 性和 学 习 能 力 两 者 进 行 了 寻 求 最 佳 的 折 衷 ， 以 获 得 最 好 的 泛 化 能 力 。 SVM 的 基 本思 想 是 把 训 练 数 据 非 线 性 的 映 射 到 一 个 更 高 维 的 特 征 空 间 （ Hilbert 空 间 ） 中 ， 在这 个 高 维 的 特 征 空 间 中 寻 找 到 一 个 超 平 面 使 得 正 例 和 反 例 两 者 间 的 隔 离边缘被最 大化 。SVM 的 出 现有 效的 解决了 传统 的 神经网络结 果选择问题、局部极小 值、过拟合等 问题。 并且在 小 样 本 、非 线 性 、数 据 高 维 等 机 器学 习 问题中 表现出 很 多令 人 注 目 的 性 质 ， 被广 泛 地 应 用 在 模 式 识 别 ， 数 据 挖 掘 等 领 域 (张 学 工 2000； 崔伟 东 2001)。 支 持 向 量 机 可 以 用 于 分 类 和 回 归 问题， 本 章 着 重 介 绍 分 类 相 关 的 知识 。 3.1 SVM 的基本思想 3.1.1 最优分类面 SVM 是 由 线 性 可 分 情 况 的 最 优 分 类 面 发 展 而 来 的 ， 用 于 两 类 问题的 分 类 。 下面 用 一 个 二 维 两 类 问题来 说 明 SVM 基 本 思 想 (白 鹏 等 ， 2008)。 图3.1 最优超平面示意图 C1 和C2 代表两类数据样本，各样本在二维中显示如图3.1， 图中的直线P0,P1就是分类函数。如果一个线性函数就完全可以把两类所有样本分开，那么就称这些数据是线性可分的；否则称非线性可分。假设两类线性可分的训练数据样本{(ᵆ1, ᵆ1), (ᵆ2, ᵆ2), … (ᵆᵄ, ᵆᵄ)}, xᵅ ∈ ᵄᵅ(d 代表样本xᵅ的长度), yᵅ...