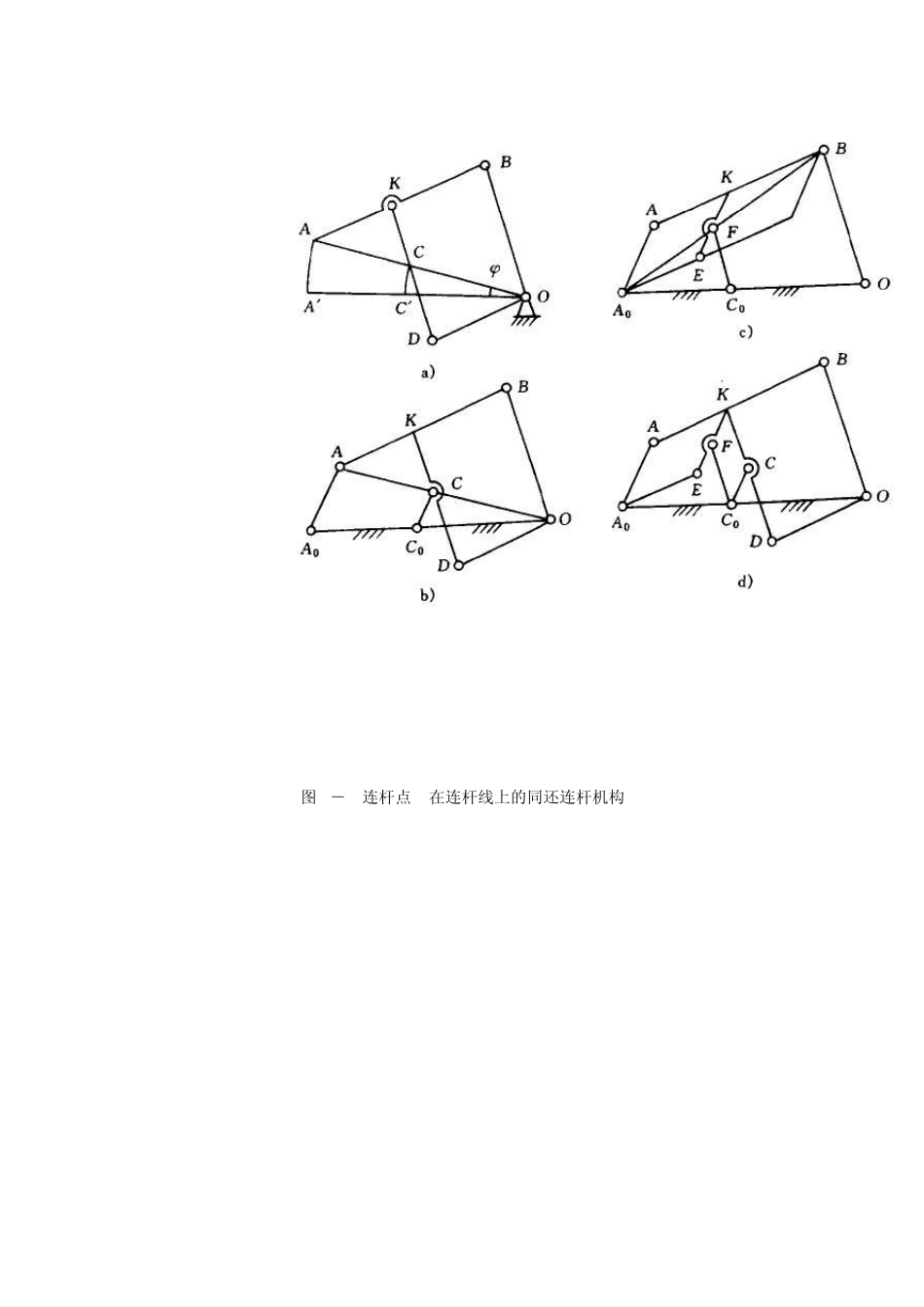
第七章 机构创新设计 第一节 同轨迹连杆机构 第二节 新型内燃机的开发 第三节 联轴器的创新设计 第四节 抓斗的原理方案创新设计 第五节 过载保护装置的机械结构设计 实例 第一节 同轨迹连杆机构 同轨迹四连杆机构是指自由度 f相同、输入构件的运动规律相同、输出构件上的一点轨迹相同的一组连杆机构,但这组连杆机构的运动学尺寸不同,所以其受力状态、动态性能有巨大差异。因而,同轨迹连杆机构的形成方法是机构创新设计的重要方法之一。 形成同轨迹连杆机构的罗伯特-契贝谢夫定理是由美国数学家萨姆尔·罗伯特于 1875年和俄国学者契贝谢夫于 1878年分别发现的,因此称为“罗伯特-契贝谢夫定理”。该定理的内容是:由一个四杆铰链机构发生的一条连杆曲线,还可以由另外两个四杆铰链机构发生出来。或表述为同一连杆曲线,可以用三个不同的机构来实现。 1.连杆点k位于连杆两铰链连线上的同迹连杆机构 图形缩放原理如下图7-1a所示为一平行四边形机构,由平行四边形obkd与机架在o 点铰接而成。a 点为bk杆延长线上的一点。连接ao得交点c。当a 点沿任意给定轨迹运动时,c点将给出与a 点相似但缩小了的轨迹。⑴ao 除以co与ab除以kb的值是相等的为常数 m(射线定理)。⑵当此四边形作为一刚体绕 o 转动一角度时,a 点转到 a',按射线定理有 aa'与cc'的比值与ao 与co的比例等于常数 m。a 点的一切运动都是这两部分运动的合成。因此 c点的运动是以缩小的比例模拟 a点的运动,反之亦然。 图7-1 连杆点k在连杆线上的同还连杆机构 第一个同迹连杆机构设计如图7-1b所示,在原始机构上作平行四边形导引机构bodk。曲柄 c0cdo为所示的第一个同迹连杆机构,k为连杆cd延长线上的点。所示曲柄拉摇杆机构的尺寸,如图中下面的公式。 第二个同迹连杆机构设计如图7-1c所示,在原始机构上作平行四边形导引机构a0ake。双摇杆机构a0efco为所 求的第二个同迹连杆机构。第三个同迹连杆机构设计如图7-1d所示,co是两具同迹连杆机构中共同的新机架的固定铰链点,机架的三个固定铰链点 a0与 o,a0与co,o与 co。 2.任意连杆点 k的同迹连杆机构 在图7-2a中,四杆机构a0a1b1b0为 a1b1上有附加连杆点 k的原始机构。由罗伯特-契贝谢夫定理决定的另两个四杆机构为 a0a2c2c0和b0b3c3c0。在这3个同迹连杆机构中有四个相似三角形;有三个不同的平行四边形。 获得两个同迹连杆机构尺寸的a·凯莱作图法:想象 7-2a中机架铰...