核反应堆物理分析习题答案第四章

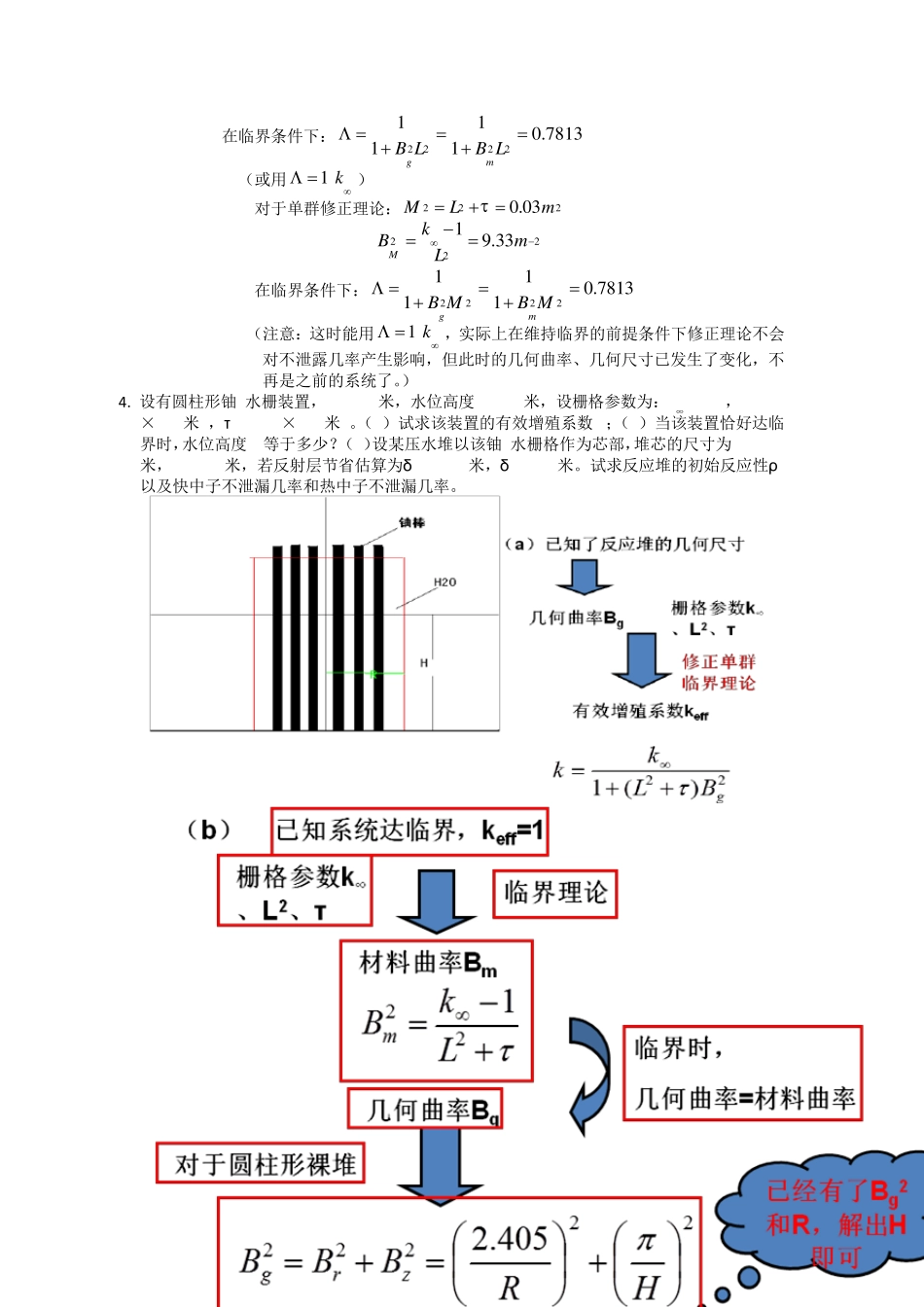
第四章 1.试求边长为, ,a b c（包括外推距离）的长方体裸堆的几何曲率和中子通量密度的分布。设有一边长 0.5 ,0.6abm cm（包括外推距离）的长方体裸堆，0.043 ,Lm 426 10m。（1）求达到临界时所必须的k ；（2）如果功率为15000,4.01fkWm ，求中子通量密度分布。 解：长方体的几何中心为原点建立坐标系，则单群稳态扩散方程为： 222222()0aaDkxyz  边界条件： ( / 2, , )( , / 2, )( , , / 2)0ay zx bzx y c （以下解题过程都不再强调外推距离，可认为所有外边界尺寸已包含了外推距离） 因为三个方向的通量拜年话是相互独立的，利用分离变量法： ( , , )( ) ( ) ( )x y zX x Y y Z z 将方程化为：22221kXYZXYZL   设：222222,,xyzXYZBBBXYZ    想考虑 X 方向，利用通解：( )cossinxxX xAB xCB x 代入边界条件：1cos()0,1,3.5,...2xnxxanABBnBaa 同理可得：0( , , )cos()cos()cos()x y zxyzaaa 其中0 是待定常数。 其几何曲率：22222()()()106.4gBmabc （1）应用修正单群理论，临界条件变为：221gkBM   其中：2220.00248MLm 1.264k （2）只须求出通量表达式中的常系数0 3222002222cos()cos()cos()()abcabcffffffVPEdVEx dxy dyz dzEabcabc31 82102()1.007 10ffPm sEabc 2.设一重水—铀反应堆的堆芯222221.28,1.8 10,1.20 10kLmm 。试按单群理论，修正单群理论的临界方程分别求出该芯部的材料曲率和达到临界时候的总的中子不泄露几率。 解：对于单群理论： 在临界条件下：2222110 .7 8 1 311gmB LB L  （或用1 k ） 对于单群修正理论：2220 .0 3MLm 22219 .3 3MkBmL  在临界条件下：2222110 .7 8 1 311gmB MB M  （注意：这时能用1 k ，实际上在维持临界的前提条件下修正理论不会对不泄露几率产生影响，但此时的几何曲率、几何尺寸已发生了变化，不再是之前的系统了。） 4 . 设有圆柱形铀-水栅装置，R=0.50米，水位高度H=1.0米，设栅格参数为：k∞=1.19，L2=6.6×10-4米2，τ ...