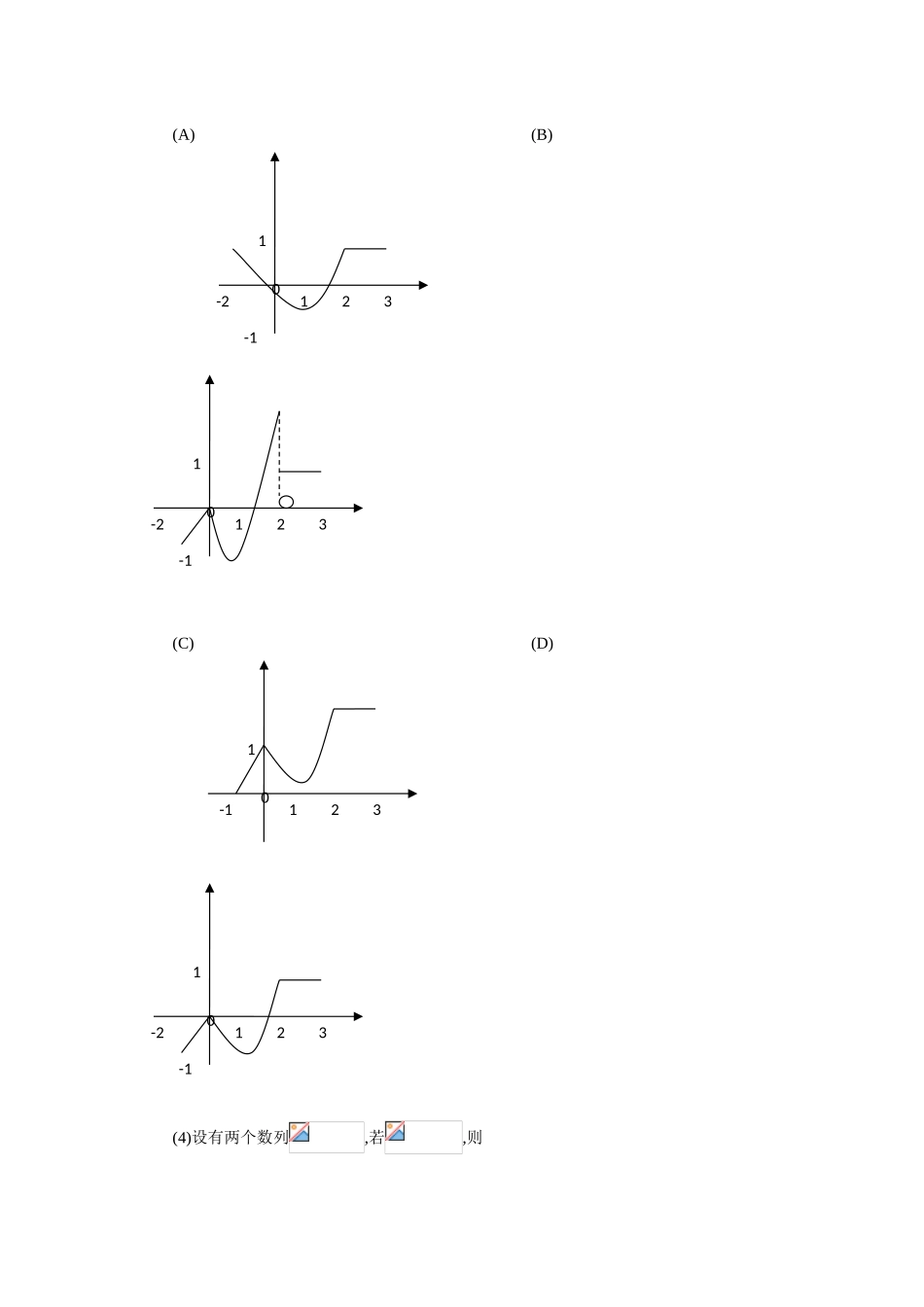
全国硕士硕士入学统一考试数学(一)试卷一、选择题(1-8 小题,每题 4 分,共 32 分,下列每题给出的四个选项中,只有一项符合题目规定,把所选项前的字母填在题后的括号内.)(1)当时,与等价无穷小,则(A) (B)(C)(D)(2)如图,正方形被其对角线划分为四个区域,,则(A) (B)(C) (D) (3)设函数在区间上的图形为则函数的图形为1-2023-1O(A)(B) (C)(D)(4)设有两个数列,若,则0231-2-110231-2-110231-110231-2-11(A)当收敛时,收敛.(B)当发散时,发散. (C)当收敛时,收敛.(D)当发散时,发散.(5) 设是 3 维 向 量 空 间的 一 组 基 , 则 由 基到 基的过渡矩阵为(A)(B) (C)(D)(6)设均为 2 阶矩阵,分别为的伴随矩阵,若,则分块矩阵的伴随矩阵为(A)(B) (C)(D)(7)设随机变量的分布函数为,其中为原则正态分布函数,则(A)0(B)0.3 (C)0.7(D)1 (8)设随机变量与互相独立,且服从原则正态分布,的概率分布为,记为随机变量的分布函数,则函数的间断点个数为(A)0(B)1 (C)2(D)3二、填空题(9-14 小题,每题 4 分,共 24 分,请将答案写在答题纸指定位置上.)(9)设函数具有二阶持续偏导数,,则 .(10)若二阶常系数线性齐次微分方程的通解为,则非齐次方程满足条件的解为 .(11)已知曲线,则 .(12)设,则 .(13)若 3 维列向量满足,其中为的转置,则矩阵的非零特征值为 .(14)设为来自二项分布总体的简单随机样本,和分别为样本均值和样本方差.若为的无偏估计量,则 .三、解答题(15-23 小题,共 94 分.请将解答写在答题纸指定的位置上.解答应写出文字阐明、证明过程或演算环节.)(15)(本题满分 9 分)求二元函数的极值.(16)(本题满分 9 分)设为 曲 线与所 围 成 区 域 的 面 积 , 记,求与的值.(17)(本题满分 11 分)椭 球 面是 椭 圆绕轴 旋 转 而 成 , 圆 锥 面是 过 点且 与 椭 圆相切的直线绕轴旋转而成.(1)求及的方程.(2)求与之间的立体体积.(18)(本题满分 11 分)(1)证明拉格朗日中值定理:若函数在上持续,在可导,则存在,使得.(2)证明:若函数在处持续,在内可导,且,则存在,且.(19)(本题满分 10 分)计算曲面积分,其中是曲面的外侧.(20)(本题满分 11 分)设,(1)求满足的.的所有向量,.(2)对(1)中的任意向量,证明无关.(21)(本题满分 11 分)设二次型.(1)求二次型的矩阵的所有特征值;(2)若二次型的规范形为,求的值.(22)(本题满分 11 分)袋中有 1 个红色球,2 个黑色球与 3 个白球,既有回放地从袋中取两次,每次取一球,...