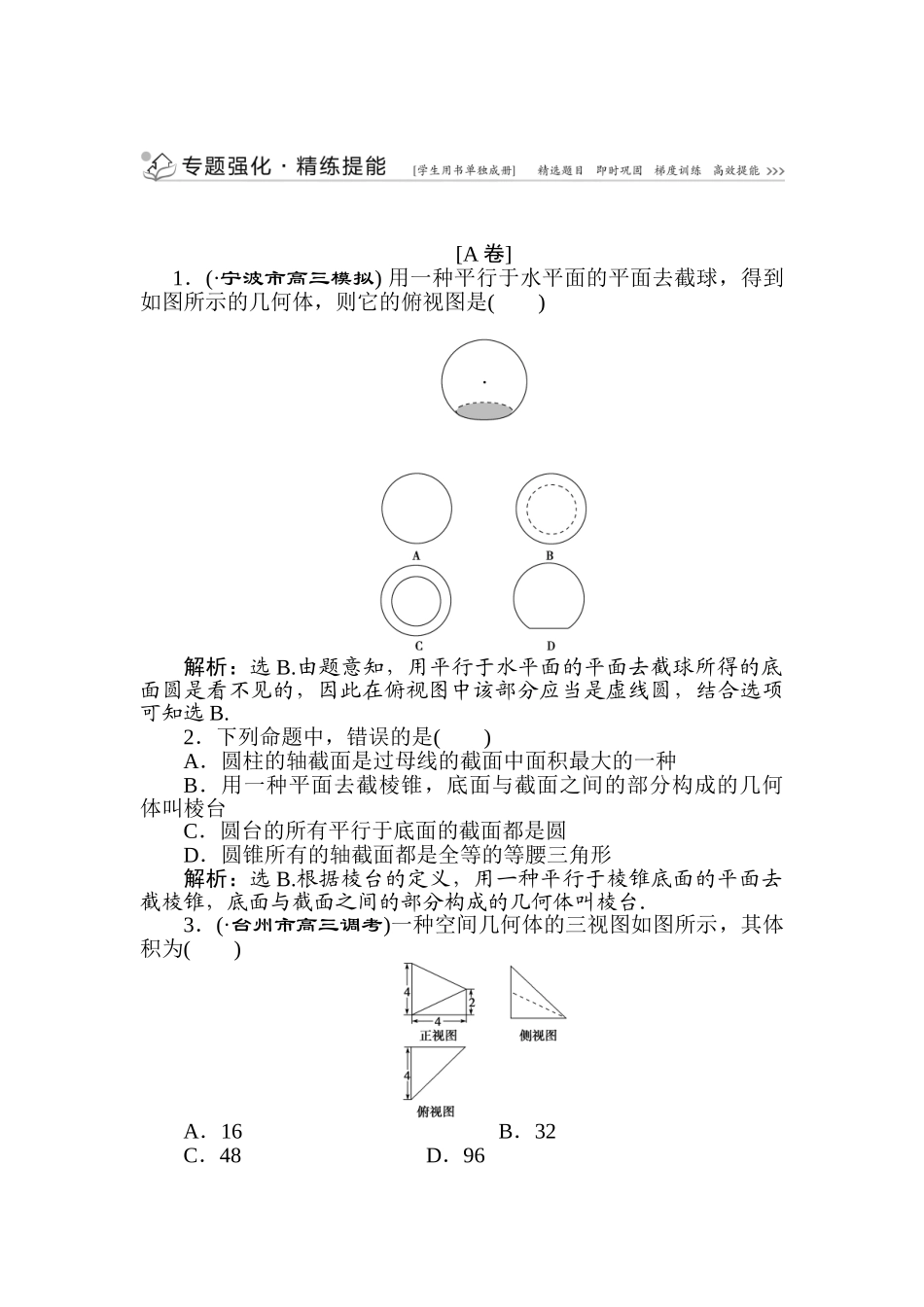
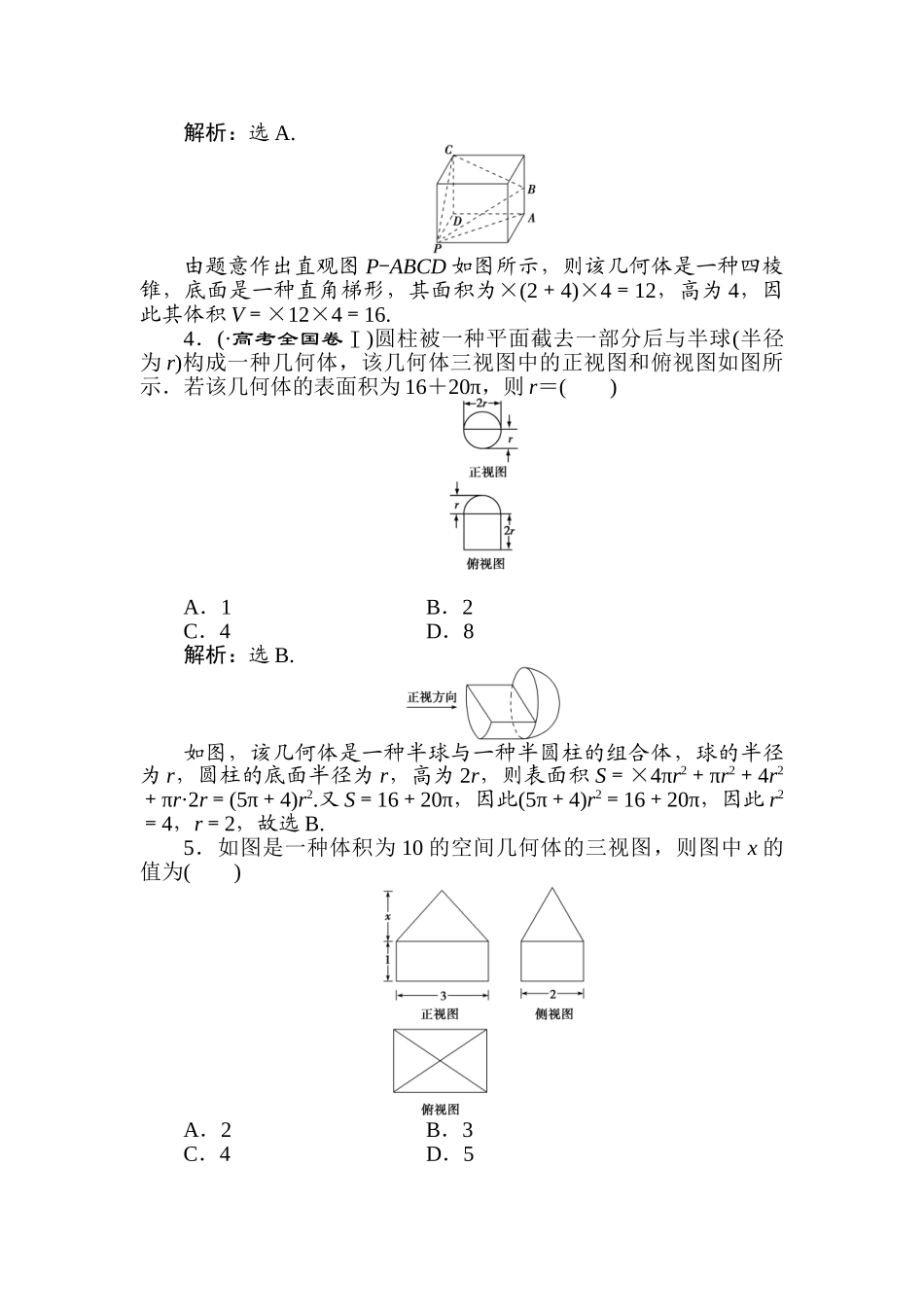
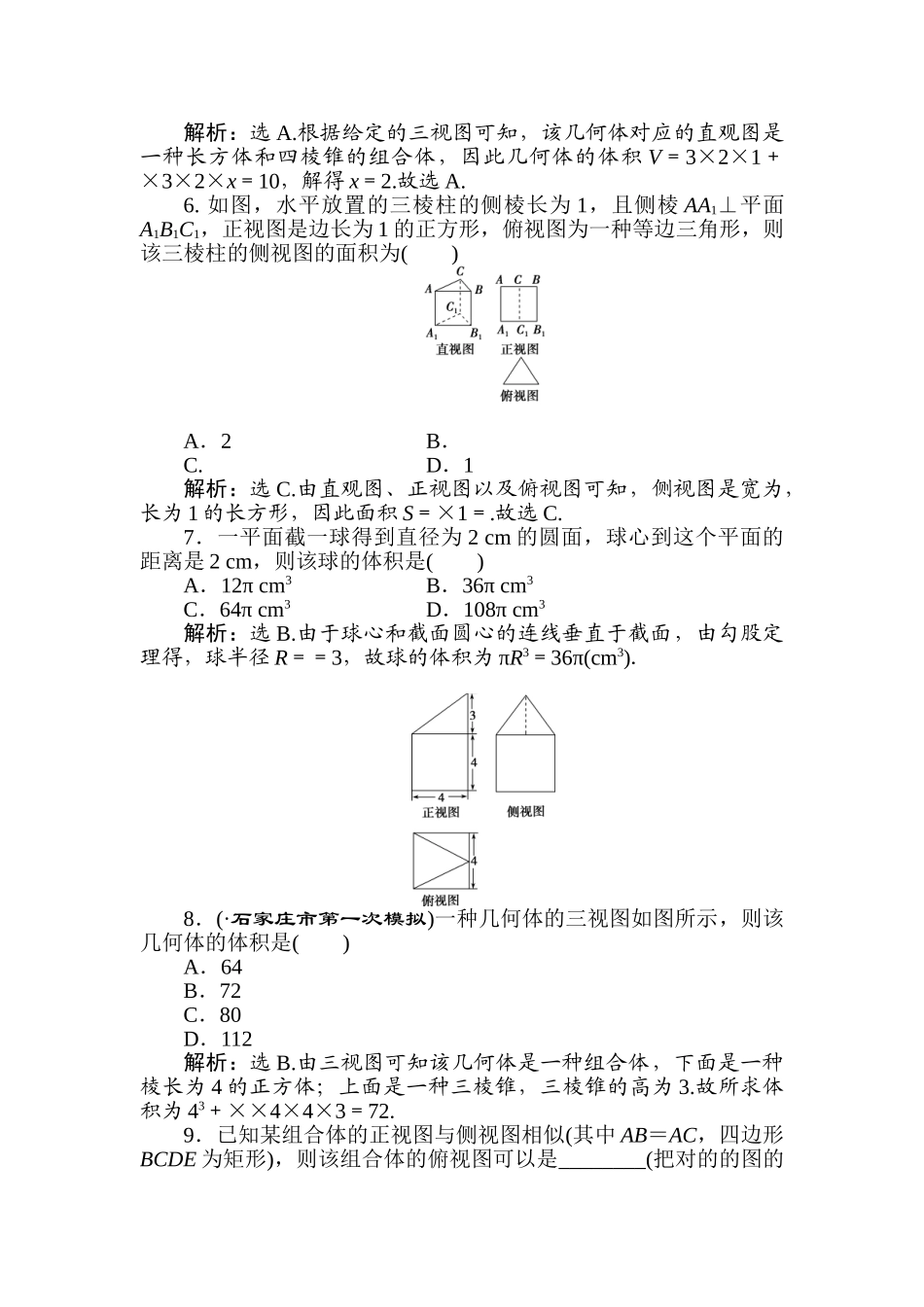
[A 卷]1.(·宁波市高三模拟) 用一种平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是( )解析:选 B.由题意知,用平行于水平面的平面去截球所得的底面圆是看不见的,因此在俯视图中该部分应当是虚线圆,结合选项可知选 B.2.下列命题中,错误的是( )A.圆柱的轴截面是过母线的截面中面积最大的一种B.用一种平面去截棱锥,底面与截面之间的部分构成的几何体叫棱台C.圆台的所有平行于底面的截面都是圆D.圆锥所有的轴截面都是全等的等腰三角形解析:选 B.根据棱台的定义,用一种平行于棱锥底面的平面去截棱锥,底面与截面之间的部分构成的几何体叫棱台.3.(·台州市高三调考)一种空间几何体的三视图如图所示,其体积为( )A.16 B.32C.48 D.96解析:选 A.由题意作出直观图 P-ABCD 如图所示,则该几何体是一种四棱锥,底面是一种直角梯形,其面积为×(2+4)×4=12,高为 4,因此其体积 V=×12×4=16.4.(·高考全国卷Ⅰ)圆柱被一种平面截去一部分后与半球(半径为 r)构成一种几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为 16+20π,则 r=( )A.1 B.2C.4 D.8解析:选 B.如图,该几何体是一种半球与一种半圆柱的组合体,球的半径为 r,圆柱的底面半径为 r,高为 2r,则表面积 S=×4πr2+πr2+4r2+πr·2r=(5π+4)r2.又 S=16+20π,因此(5π+4)r2=16+20π,因此 r2=4,r=2,故选 B.5.如图是一种体积为 10 的空间几何体的三视图,则图中 x 的值为( )A.2 B.3C.4 D.5解析:选 A.根据给定的三视图可知,该几何体对应的直观图是一种长方体和四棱锥的组合体,因此几何体的体积 V=3×2×1+×3×2×x=10,解得 x=2.故选 A.6. 如图,水平放置的三棱柱的侧棱长为 1,且侧棱 AA1⊥平面A1B1C1,正视图是边长为 1 的正方形,俯视图为一种等边三角形,则该三棱柱的侧视图的面积为( )A.2 B.C. D.1解析:选 C.由直观图、正视图以及俯视图可知,侧视图是宽为,长为 1 的长方形,因此面积 S=×1=.故选 C.7.一平面截一球得到直径为 2 cm 的圆面,球心到这个平面的距离是 2 cm,则该球的体积是( )A.12π cm3 B.36π cm3C.64π cm3 D.108π cm3解析:选 B.由于球心和截面圆心的连线垂直于截面,由勾股定理得,球半径 R==3,故球的体积为 πR3=36π(cm3).8.(·石家庄市第一次模拟)一种几何体的三视图如图所...