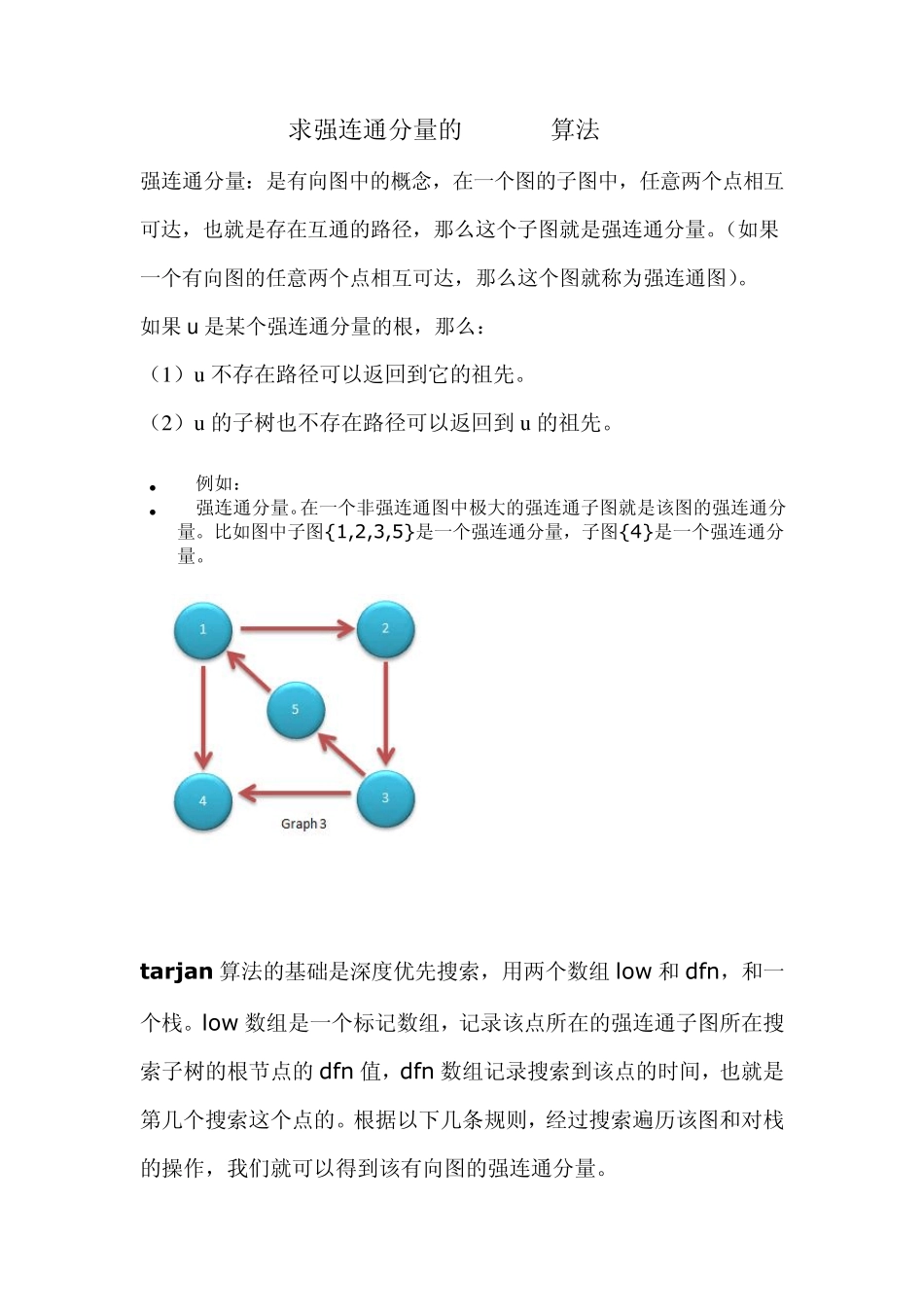
求强连通分量的tarjan算法 强连通分量:是有向图中的概念,在一个图的子图中,任意两个点相互可达,也就是存在互通的路径,那么这个子图就是强连通分量。(如果一个有向图的任意两个点相互可达,那么这个图就称为强连通图)。 如果 u 是某个强连通分量的根,那么: (1 )u 不存在路径可以返回到它的祖先。 (2 )u 的子树也不存在路径可以返回到 u 的祖先。 例如: 强连通分量。在一个非强连通图中极大的强连通子图就是该图的强连通分量。比如图中子图{1,2,3,5}是一个强连通分量,子图{4}是一个强连通分量。 tarjan 算法的基础是深度优先搜索,用两个数组 low 和 dfn,和一个栈。low 数组是一个标记数组,记录该点所在的强连通子图所在搜索子树的根节点的dfn 值,dfn 数组记录搜索到该点的时间,也就是第几个搜索这个点的。根据以下几条规则,经过搜索遍历该图和对栈的操作,我们就可以得到该有向图的强连通分量。 算法规则: 数组的初始化:当首次搜索到点p 时,Dfn 与Low 数组的值都为到该点的时间。 堆栈:每搜索到一个点,将它压入栈顶。 当点p 有与点p’相连时,如果此时(时间为dfn[p]时)p’不在栈中,p的low 值为两点的low 值中较小的一个。 当点p 有与点p’相连时,如果此时(时间为dfn[p]时)p’在栈中,p 的low 值为p 的low 值和 p’的dfn 值中较小的一个。 每当搜索到一个点经过以上操作后(也就是子树已经全部遍历)的low值等于 dfn 值,则将它以及在它之上的元素弹出栈。这些出栈的元素组成一个强连通分量。 继续搜索(或许会更换搜索的起点,因为整个有向图可能分为两个不连通的部分),直到所有点被遍历。 算法伪代码: tarjan(u) { DFN[u]=Low[u]=++Index // 为节点u 设定次序编号和 Low 初值 Stack.push(u) // 将节点u 压入 栈中 for each (u, v) in E // 枚举每一条边 if (!dfn[v]) // 如果节点v 未被访问过 { tarjan(v) // 继续向下找 Low[u] = min(Low[u], Low[v]) } else if (v in S) // 如果节点v 还在栈内 Low[u] = min(Low[u], DFN[v]) if (DFN[u] == Low[u]) // 如果节点u 是强连通分量的根 do{ v = S.pop // 将 v 退栈,为该强连通分量中一个顶点 }while(u == v); } 演示算法流程; 从节点1 开始DFS,把遍历到的节点加入栈中。搜索到节点u=6 时,DFN[6]=LOW[6...