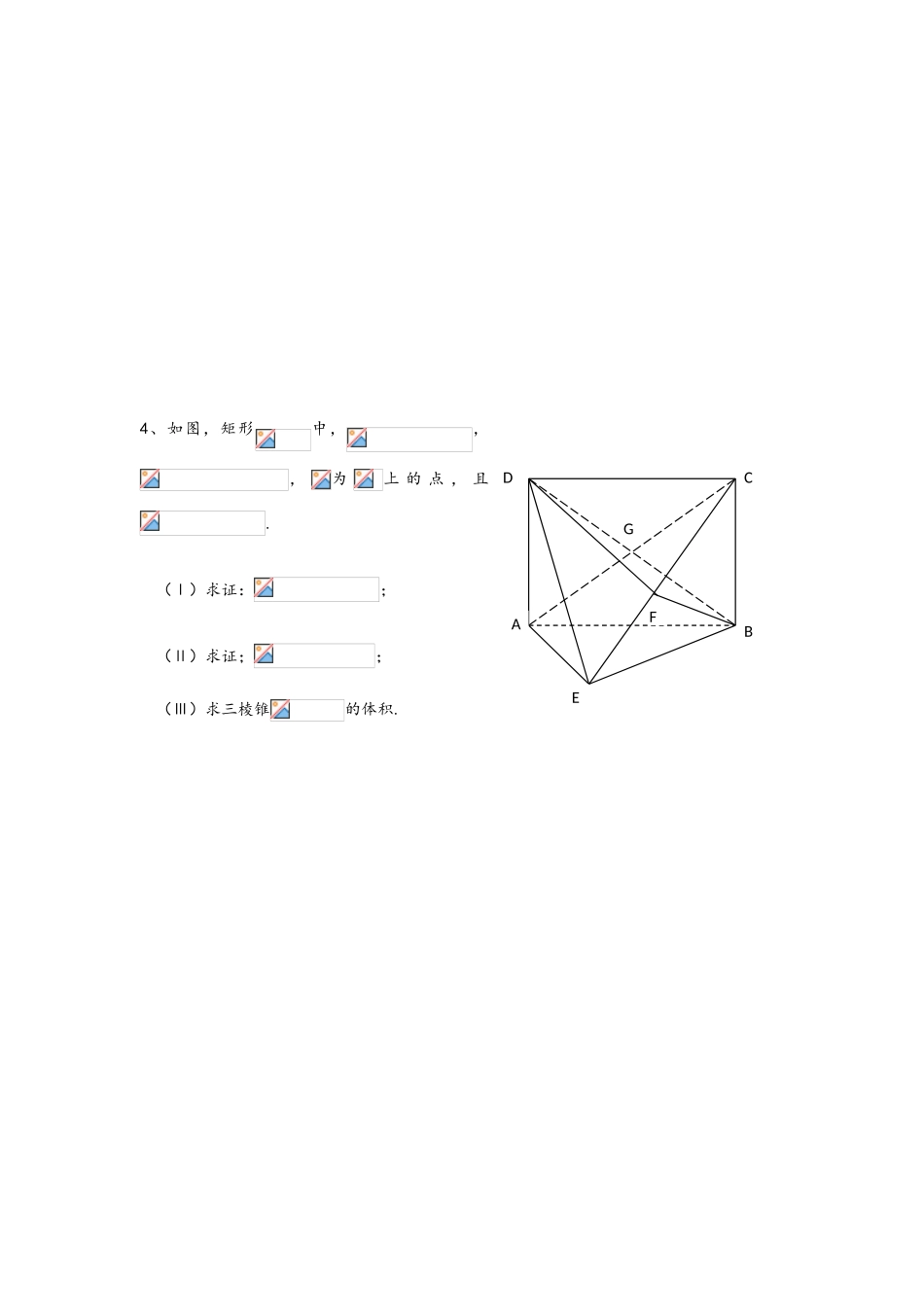
文科立体几何4、如图,矩形中,,,为上 的 点 , 且.(Ⅰ)求证:;(Ⅱ)求证;;(Ⅲ)求三棱锥的体积.ABCDEFG5、如图所示,在棱长为 2 的正方体中,、分别为、的中点.(Ⅰ)求证:平面;(Ⅱ)求证:;(III)求三棱锥的体积.6、 如图,在四棱锥中,底面 ABCD 是正方形,侧棱底面 ABCD,,E 是 PC 的中点,作交 PB 于点 F.(I) 证明: PA∥平面 EDB;(II) 证明:PB⊥平面 EFD;(III) 求三棱锥的体积.ABDEFA1B1第 7 题图7、 如图, 在三棱柱中,,平面,,,,点是的中点,(1)求证:; (2)求证:;(3)求三棱锥的体积。8. 如图,四边形 ABCD 为矩形,AD⊥平面 ABE,AE=EB=BC=2,为上的点,且 BF⊥平面 ACE.(1)求证:AE⊥BE;(2)求三棱锥 D-AEC 的体积;(3)设 M 在线段 AB 上,且满足 AM=2MB,试在线段 CE 上确定一点 N,使得 MN∥平面 DAE.BCADEFM9、如图,在四棱锥 P—ABCD 中,底面 ABCD 是菱形,∠ABC=60°,PA=AC=a,PB=PD=,点 E,F 分别在 PD,BC 上,且 PE:ED=BF:FC。 (1)求证:PA⊥平面 ABCD; (2)求证:EF//平面 PAB。10、正方形所在平面与三角形所在平面相交于,平面,且,. (1)求证:平面;(2)求凸多面体的体积. ABCDE11、如图的几何体中,平面,平面,△为等边三角形, ,为的中点.(1)求证:平面;(2)求证:平面平面;(3)求这个几何体的体积.1213、已知直角梯形 ABCD 中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+,过 A 作 AE⊥CD,垂足为 E,G、F 分别为 AD、CE 的中点,现将△ADE 沿 AE 折叠,使 DE⊥EC.(1)求证:BC⊥平面 CDE;(2)求证:FG∥平面 BCD;(3)求四棱锥 D-ABCE 的体积.17、如图 4,在边长为 1 的等边三角形中,分别是边上的点,,是的中点,与交于点,将沿折起,得到如图 5 所示的三棱锥,其中.(1) 证明://平面;图 4GEFABCD(2) 证明:平面;(3) 当时,求三棱锥的体积. 18、如图,直三棱柱 ABC-A1B1C1中,D,E 分别是 AB,BB1的中点.(1) 证明: BC1//平面 A1CD;(2) 设 AA1= AC=CB=2,AB=2,求三棱锥 C 一 A1DE 的体积.图 5DGBFCAE19 、 如 图 , 四 棱 锥的 底 面是 边 长 为 2 的 菱 形 ,. 已 知 .(Ⅰ)证明:(Ⅱ)若为的中点,求三菱锥的体积.19.G1、G4、G3[·安徽卷] 如图 15 所示,四棱锥 P ABCD 的底面是边长为 8 的正方形,四条侧棱长均为 2.点 G,E,F,H 分别...