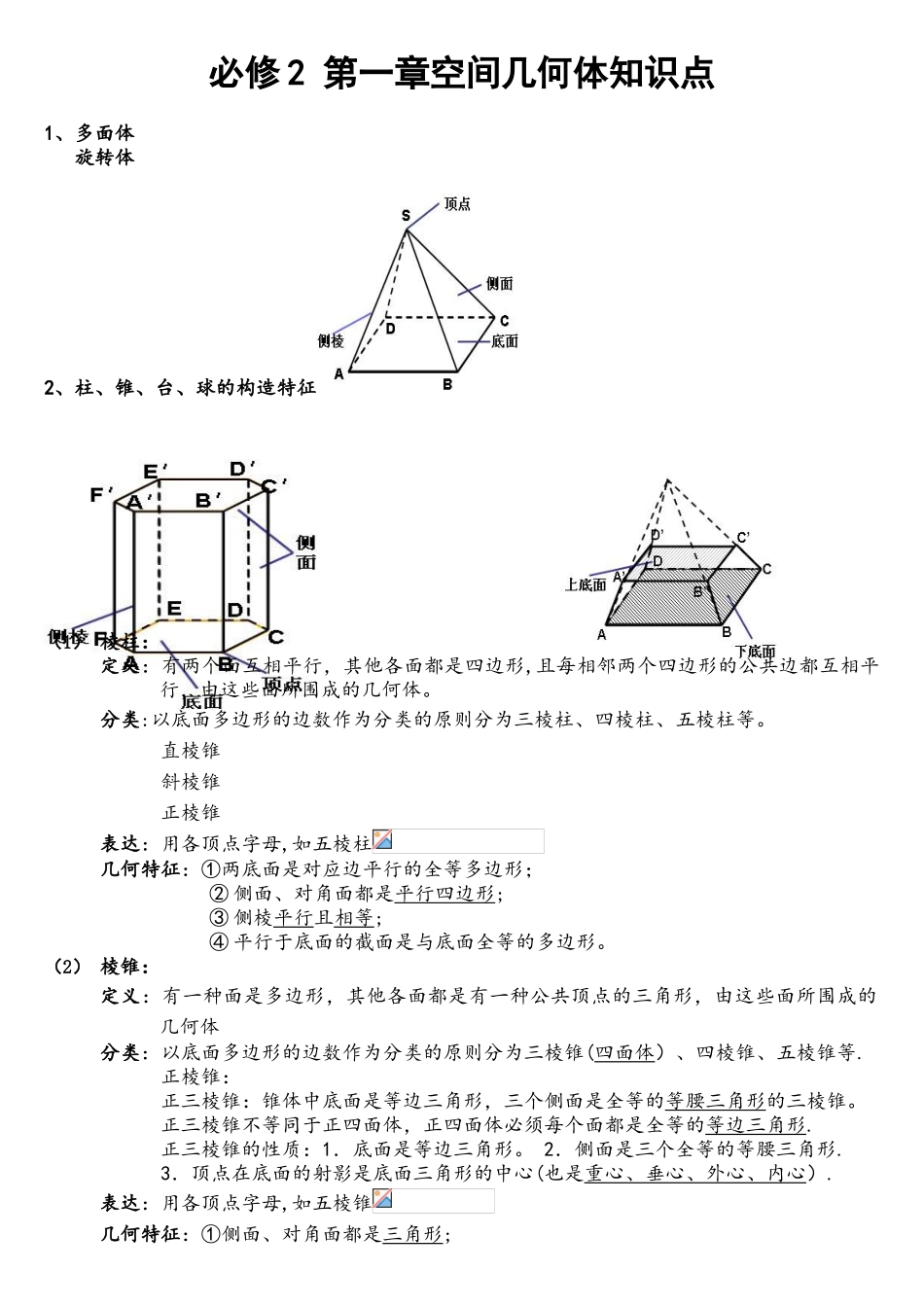
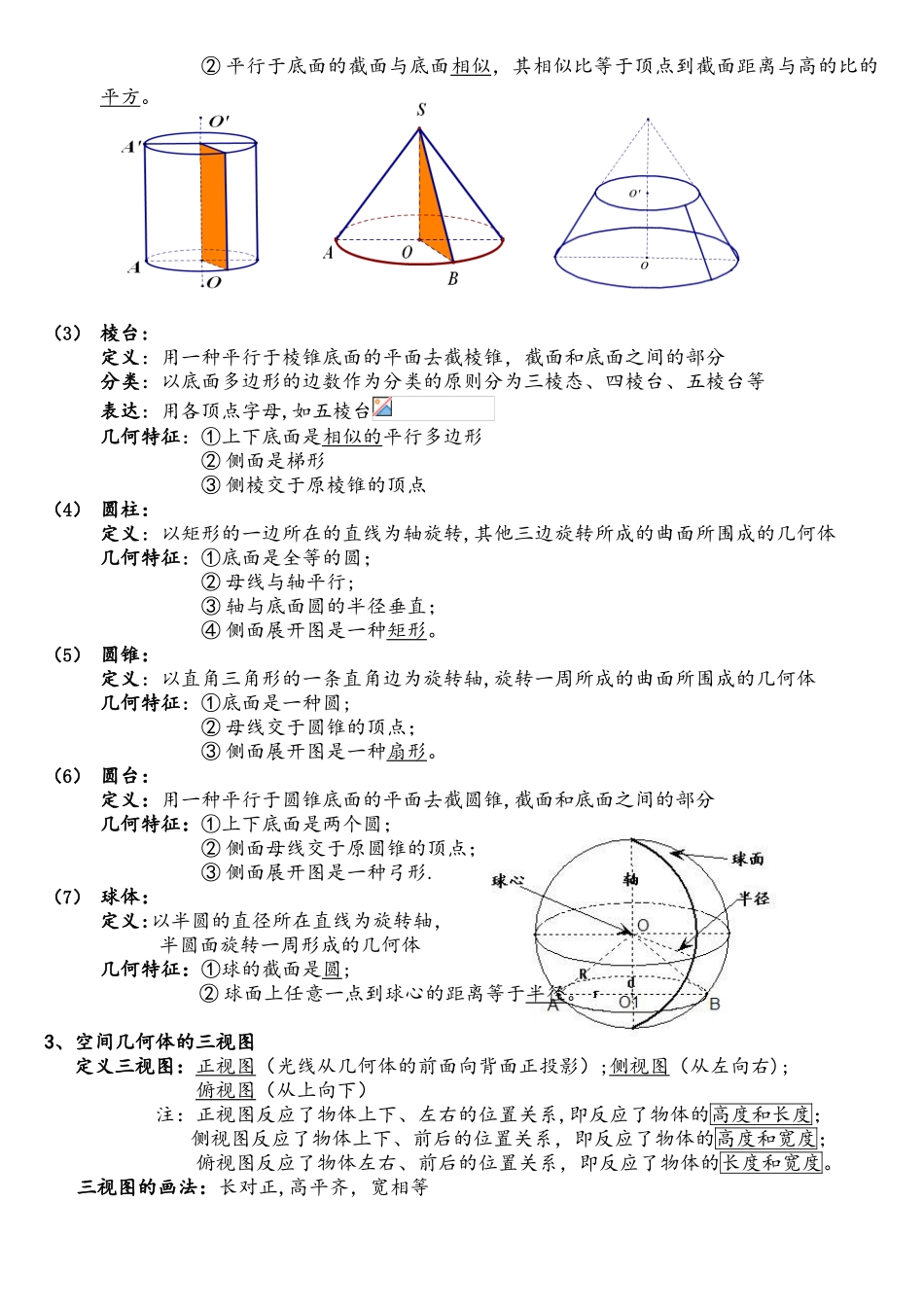
必修 2 第一章空间几何体知识点1、多面体 旋转体2、柱、锥、台、球的构造特征(1) 棱柱:定义:有两个面互相平行,其他各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。分类:以底面多边形的边数作为分类的原则分为三棱柱、四棱柱、五棱柱等。 直棱锥 斜棱锥 正棱锥表达:用各顶点字母,如五棱柱 几何特征:①两底面是对应边平行的全等多边形;② 侧面、对角面都是平行四边形;③ 侧棱平行且相等;④ 平行于底面的截面是与底面全等的多边形。(2) 棱锥:定义:有一种面是多边形,其他各面都是有一种公共顶点的三角形,由这些面所围成的几何体分类:以底面多边形的边数作为分类的原则分为三棱锥(四面体)、四棱锥、五棱锥等. 正棱锥:正三棱锥:锥体中底面是等边三角形,三个侧面是全等的等腰三角形的三棱锥。正三棱锥不等同于正四面体,正四面体必须每个面都是全等的等边三角形.正三棱锥的性质:1.底面是等边三角形。 2.侧面是三个全等的等腰三角形.3.顶点在底面的射影是底面三角形的中心(也是重心、垂心、外心、内心). 表达:用各顶点字母,如五棱锥几何特征:①侧面、对角面都是三角形;② 平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。(3) 棱台:定义:用一种平行于棱锥底面的平面去截棱锥,截面和底面之间的部分分类:以底面多边形的边数作为分类的原则分为三棱态、四棱台、五棱台等表达:用各顶点字母,如五棱台几何特征:①上下底面是相似的平行多边形 ② 侧面是梯形 ③ 侧棱交于原棱锥的顶点(4) 圆柱:定义:以矩形的一边所在的直线为轴旋转,其他三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;② 母线与轴平行;③ 轴与底面圆的半径垂直;④ 侧面展开图是一种矩形。(5) 圆锥:定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体几何特征:①底面是一种圆; ② 母线交于圆锥的顶点;③ 侧面展开图是一种扇形。(6) 圆台:定义:用一种平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;② 侧面母线交于原圆锥的顶点;③ 侧面展开图是一种弓形.(7) 球体:定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体几何特征:①球的截面是圆;② 球面上任意一点到球心的距离等于半径。3、空间几何体的三视图定义三视图:正视图(光线从几何体的前面向背面正投...