电磁学第8、9章作业分析2007

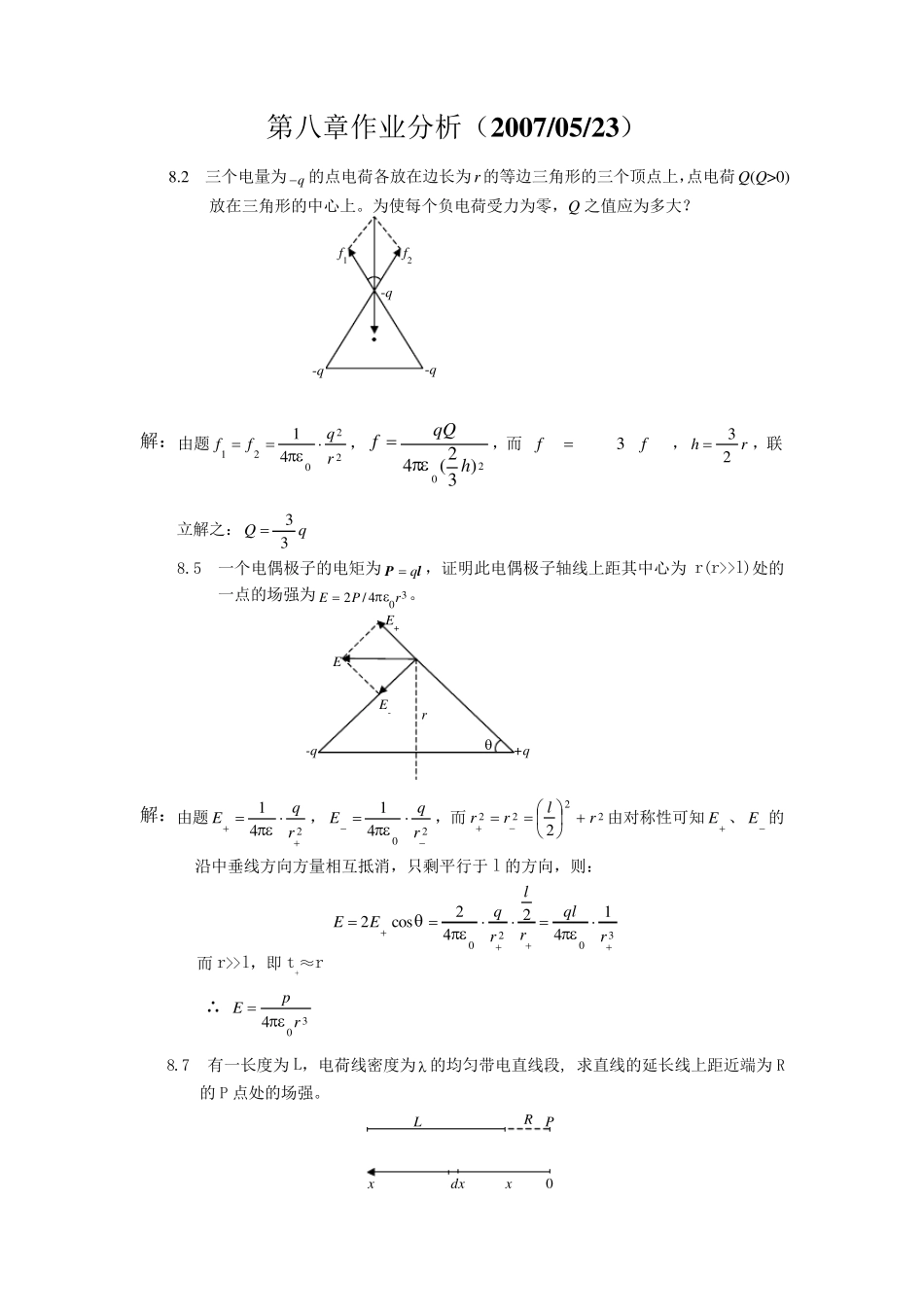
第八章作业分析（2 0 0 7 /0 5 /2 3 ） 8.2 三个电量为q 的点电荷各放在边长为r 的等边三角形的三个顶点上，点电荷Q(Q>0)放在三角形的中心上。为使每个负电荷受力为零，Q 之值应为多大？ -q -q -q f2 f1 解：由题2202141rqff，20)32(4hqQf，而ff3， rh23，联立解之： qQ33 8.5 一个电偶极子的电矩为lPq，证明此电偶极子轴线上距其中心为r(r>>l)处的一点的场强为304/2rPE。 E+ E- E r -q +q  解：由题241rqE，2041rqE，而22222rlrr由对称性可知E 、E 的沿中垂线方向方量相互抵消，只剩平行于l 的方向，则： 3020142cos2rqlrlrqEE 而r>>l，即t+≈r ∴ 304rpE 8.7 有一长度为L，电荷线密度为 的均匀带电直线段, 求直线的延长线上距近端为R的P 点处的场强。 x dx x 0 L R P 解：取线地dx 有：dxdq ∴ 2041xdxdE ∴ )(441020LRRLxdxELRR  方向沿带电直线 8.9 如图8-43，一个细的带电塑料圆环，半径为R，所带电荷线密度 和 有 sin0的关系，求在圆心处的电场强度的方向和大小。 解：取线元dl，有： dRdl ∴ )(sin414100020RdRRRdEd ∴ 0cossin42000 dREx RdREy00220004sin4  8.11 如图8-45 所示，有宽度为L，电荷面密度为σ的无限长均匀带电平面，求在与带电平面共面的P 点处的场强。 dx x x  P 解： 取宽度为dx 的无限长，其在P 点的场强为： xaLdxrdE121200 方向均垂直于带长方向且向外 ∴ LLaLxRLdxE000ln22 8.13 (1) 点电荷 q 位于边长为 a 的正方体的中心，通过此立方体的每一面的 E 通量各是多少？ (2) 若电荷移至正立方体的一个项点上，那么通过每个平面的 E 通量又各是多少？ 解：(1) 由对称性可知立方体的六个面对中心完全对称，应平分总通量 06qe  (2) 若移至某一顶点则与该顶点相连的三个面由于E始终在面内所以0e，而另三个面的通量可用补的思想，设法把此顶点置于一个更大的立方体中心，则此时那三个面完全对称地占了总通量的241461，即024qe  8.15 在 图...