电路原理作业第四章

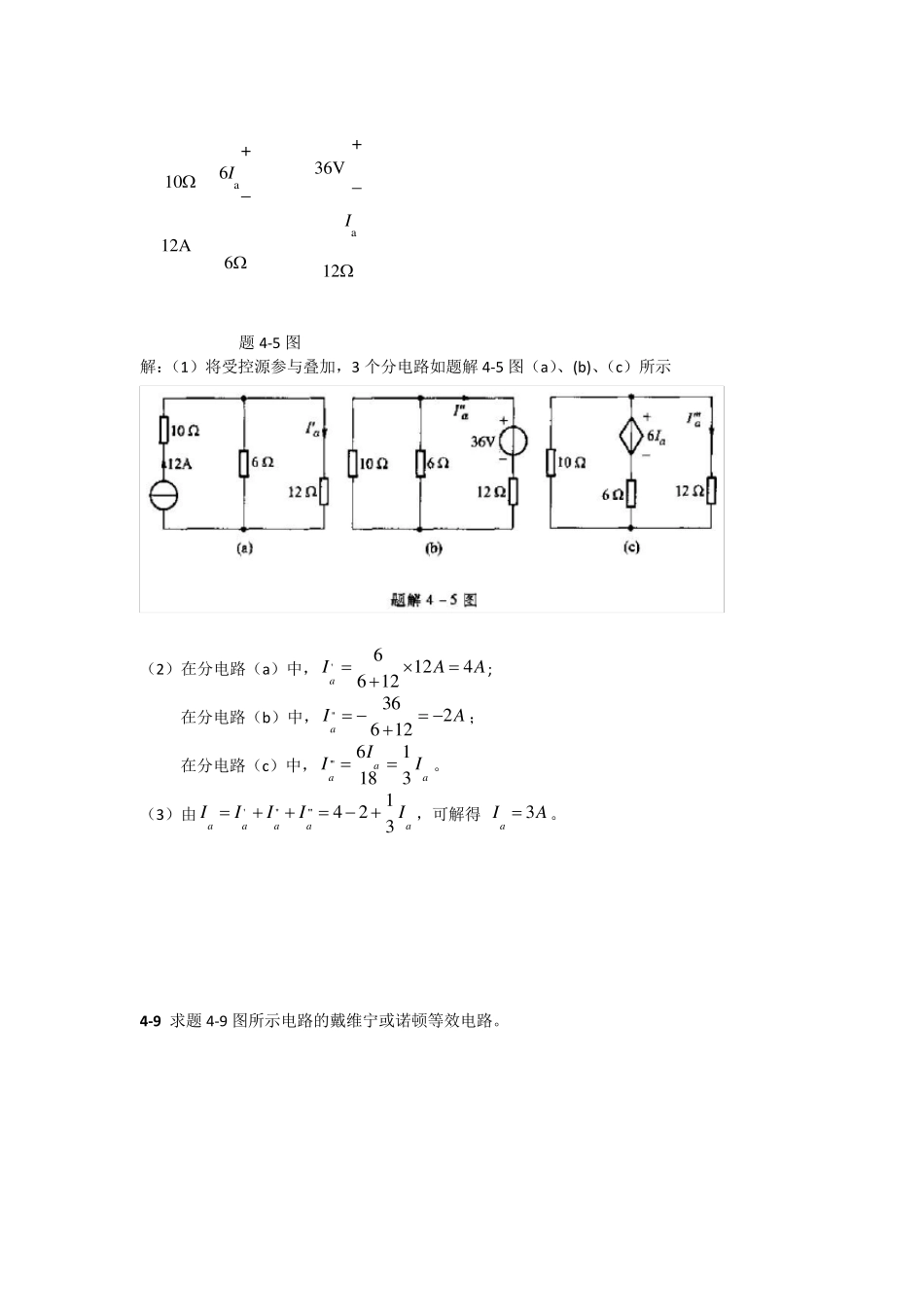
第四章“电路定理”练习题 4-2 应用叠加定理求题 4-2 图所示电路中电压 u 。 +240u50V+136V8103A+ 题 4-2 图 题解 4-2 图 解：画出电源分别作用的分解电路，如图解 4-2 图（a）和（b）所示 对题解图 4-2（a）应用结点电压法有 111113650()8240108210nu 解得2u(1)113.650.10.0250.1nuu = 18.60.225 = 24882.6673V 对题解图 4-2（b）应用电阻串并联化简方法，可求得 10 402 (8)381610403310 40183(8)21040iSuV   (2)16182323isuuV   所以，由叠加定理得原电路的 u 为 (1)(2)248824080333uuuV 4-5 应用叠加定理，按下列步骤求解题 4-5 图中aI 。（1）将受控源参与叠加，画出三个分电路，第三分电路中受控源电压为a6I ，aI 并非分响应，而为未知总响应；（2）求出三个分电路的分响应aI 、aI 、aI  ，aI  中包含未知量aI ；（3）利用aaaaIIII解出aI 。 +6Ia6Ia+36V101212A 题4-5 图 解：（1）将受控源参与叠加，3 个分电路如题解4-5 图（a）、(b)、（c）所示 （2）在分电路（a）中，'61246 12aIAA; 在分电路（b）中，''3626 12aIA  ； 在分电路（c）中，'''61183aaaIII。 （3）由''''''1423aaaaaIIIII，可解得 3aIA。 4-9 求题4-9 图所示电路的戴维宁或诺顿等效电路。 ba1A223V+4 （a） 1'15V67+10952 （b） 题4-9 图 解：（1 ） 求开路电压ocu。设ocu参考方向如题4-9（a）图所示，由KVL列方程 24 I32I 1)=0 （ 解得 1I=- 8 A 144 ()0.58ocuIV   求等效电阻eqR。将原图中电压源短路，电流源开路,电路变为题解4-9（a）图（a)应用电阻串并联等效，求得 (22) / 42eqR  题解4-9 （a）图 画出戴维宁等效电路如题解4-9 （a）图（b）所示，应用电源等效变换得诺顿等效电 路如题解4-9 （a）图（c）所示，其中 0.50.252ocscequIAR  （2）本题电路为梯形电路，根据齐性定理，应用“倒退法”求开路电压ocu。 设'10ococuuV,各支路电流如题4-9(b)图所示，计算得 '5510110iiA '22(210) 112nnuuV  ''244122.455nuiiA '''33452.413.4iiiiA  '''113...