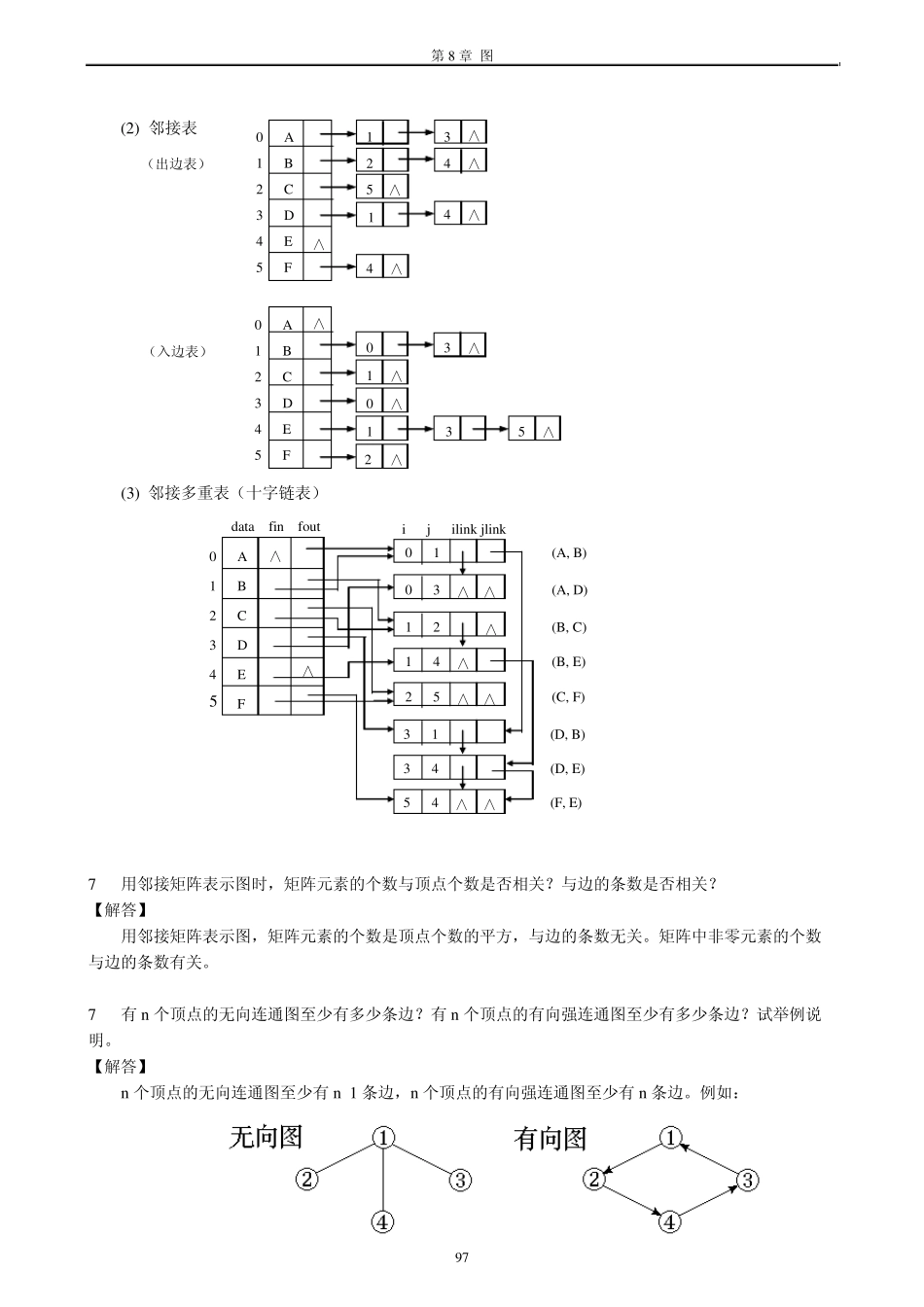
第8 章 图 96 010000000000010010100000010100001010Edge第7 章 图 7-1 画出1 个顶点、2 个顶点、3 个顶点、4 个顶点和5 个顶点的无向完全图。试证明在n 个顶点的无向完全图中,边的条数为n (n -1)/2。 【解答】 【证明】 在有n 个顶点的无向完全图中,每一个顶点都有一条边与其它某一顶点相连,所以每一个顶点有n -1条边与其他n -1 个顶点相连,总计n 个顶点有n (n -1)条边。但在无向图中,顶点i 到顶点j 与顶点j 到顶点i 是同一条边,所以总共有n (n -1)/2 条边。 7-2 右边的有向图是强连通的吗?请列出所有的简单路径。 【解答】 判断一个有向图是否强连通,要看从任一顶点出发是否能够回到该顶点。右面的有向图做不到这一点,它不是强连通的有向图。各个顶点自成强连通分量。 所谓简单路径是指该路径上没有重复的顶点。 从顶点A 出发,到其他的各个顶点的简单路径有A→B,A→D→B,A→B→C,A→D→B→C,A→D,A→B→E,A→D→E,A→D→B→E,A→B→C→F→E,A→D→B→C→F→E,A→B→C→F,A→D→B→C→F。 从顶点B 出发,到其他各个顶点的简单路径有B→C,B→C→F,B→E,B→C→F→E。 从顶点C 出发,到其他各个顶点的简单路径有C→F,C→F→E。 从顶点D 出发,到其他各个顶点的简单路径有D→B,D→B→C,D→B→C→F,D→E,D→B→E,D→B→C→F→E。 从顶点E 出发,到其他各个顶点的简单路径无。 从顶点F 出发,到其他各个顶点的简单路径有F→E。 7-3 给出右图的邻接矩阵、邻接表和邻接多重表表示。 【解答】 (1) 邻接矩阵 1 个顶点的 无向完全图 2 个顶点的 无向完全图 3 个顶点的 无向完全图 4 个顶点的 无向完全图 5 个顶点的 无向完全图 A B C D E F A B C D E F 第8 章 图 97 (2) 邻接表 (3) 邻接多重表(十字链表) 7-4 用邻接矩阵表示图时,矩阵元素的个数与顶点个数是否相关?与边的条数是否相关? 【解答】 用邻接矩阵表示图,矩阵元素的个数是顶点个数的平方,与边的条数无关。矩阵中非零元素的个数与边的条数有关。 7-5 有n 个顶点的无向连通图至少有多少条边?有n 个顶点的有向强连通图至少有多少条边?试举例说明。 【解答】 n 个顶点的无向连通图至少有n-1 条边,n 个顶点的有向强连通图至少有n 条边。例如: 0 A 1 B 2 C 3 D 4 E 5 F 1 0 A 1 B 2 ...