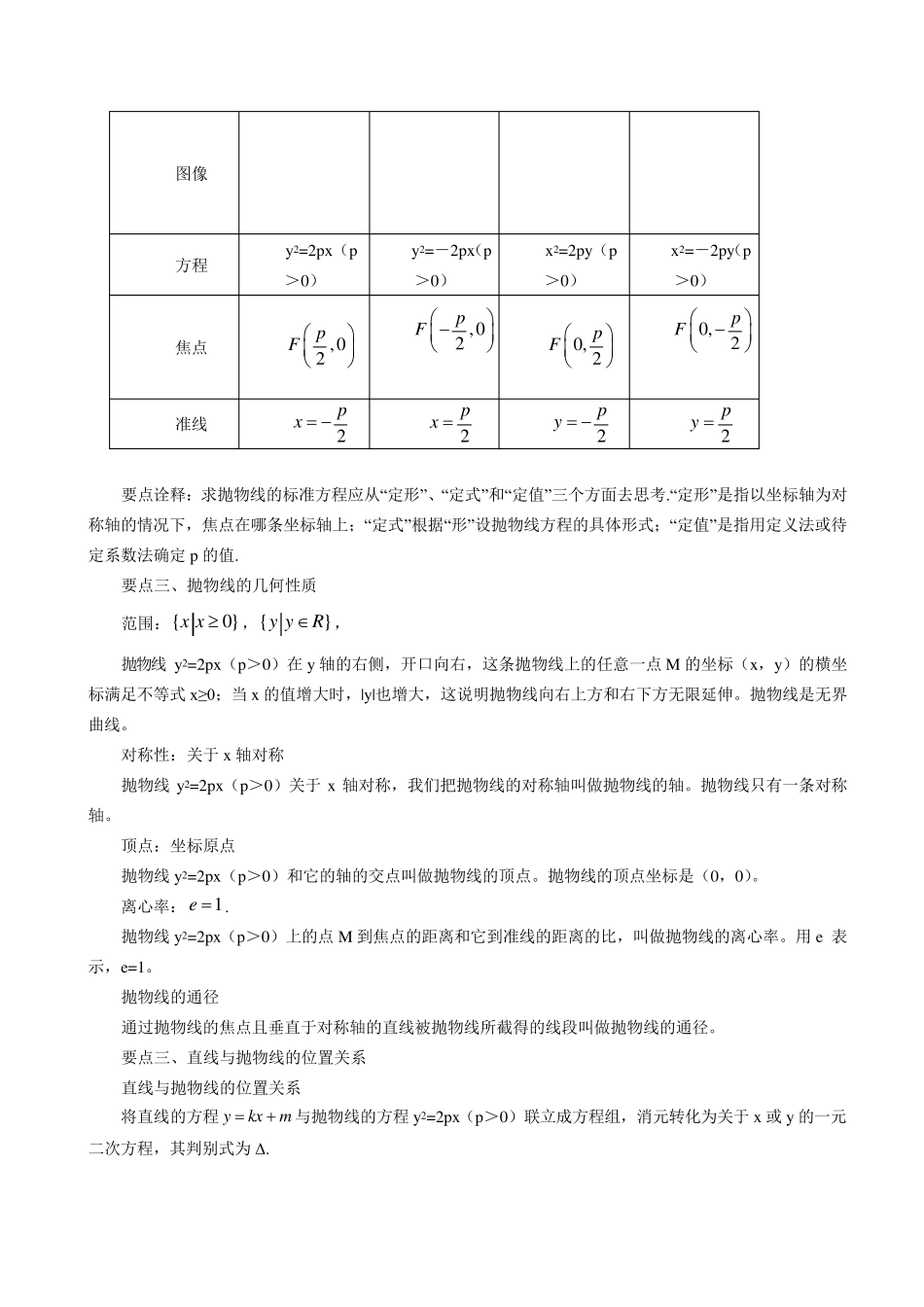
直线与抛物线的位置关系 【学习目标】 1.能正熟练使用直接法、待定系数法、定义法求抛物线的方程; 2.能熟练运用几何性质(如范围、对称性、顶点、离心率、准线)解决相关问题; 3.能够把直线与抛物线的位置关系的问题转化为方程组解的问题,判断位置关系及解决相关问题. 【知识网络】 【要点梳理】 要点一、抛物线的定义 定义:平面内与一个定点F 和一条定直线l(l 不经过点F )的距离相等的点的轨迹叫做抛物线,定点F 叫做抛物线的焦点,定直线l 叫做抛物线的准线. 要点诠释:上述定义可归结为“一动三定”:一个动点,一定点F(即焦点),一定直线(即准线),一定值 1(即动点M 到定点F 的距离与定直线l的距离之比). 要点二、抛物线的标准方程 抛物线标准方程的四种形式: 22ypx,22ypx ,22xpy,22xpy (0)p 抛物线 抛物线的定义与标准方程 抛物线的几何性质 直线与抛物线的位置关系 抛物线的综合问题 抛物线的弦问题 抛物线的准线 图像 方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0) 焦点 ,02pF ,02pF 0, 2pF 0,2pF 准线 2px 2px 2py 2py 要点诠释:求抛物线的标准方程应从“定形”、“定式”和“定值”三个方面去思考.“定形”是指以坐标轴为对称轴的情况下,焦点在哪条坐标轴上;“定式”根据“形”设抛物线方程的具体形式;“定值”是指用定义法或待定系数法确定p 的值. 要点三、抛物线的几何性质 范围:{0}x x ,{}y yR, 抛物线y2=2px(p>0)在 y 轴的右侧,开口向右,这条抛物线上的任意一点M 的坐标(x,y)的横坐标满足不等式 x≥0;当 x 的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸。抛物线是无界曲线。 对称性:关于 x 轴对称 抛物线y2=2px(p>0)关于 x 轴对称,我们把抛物线的对称轴叫做抛物线的轴。抛物线只有一条对称轴。 顶点:坐标原点 抛物线y2=2px(p>0)和它的轴的交点叫做抛物线的顶点。抛物线的顶点坐标是(0,0)。 离心率:1e . 抛物线y2=2px(p>0)上的点M 到焦点的距离和它到准线的距离的比,叫做抛物线的离心率。用 e 表示,e=1。 抛物线的通径 通过抛物线的焦点且垂直于对称轴的直线被抛物线所截得的线段叫做抛物线的通径。 要点三、直线与抛物线的位置关系 直线...