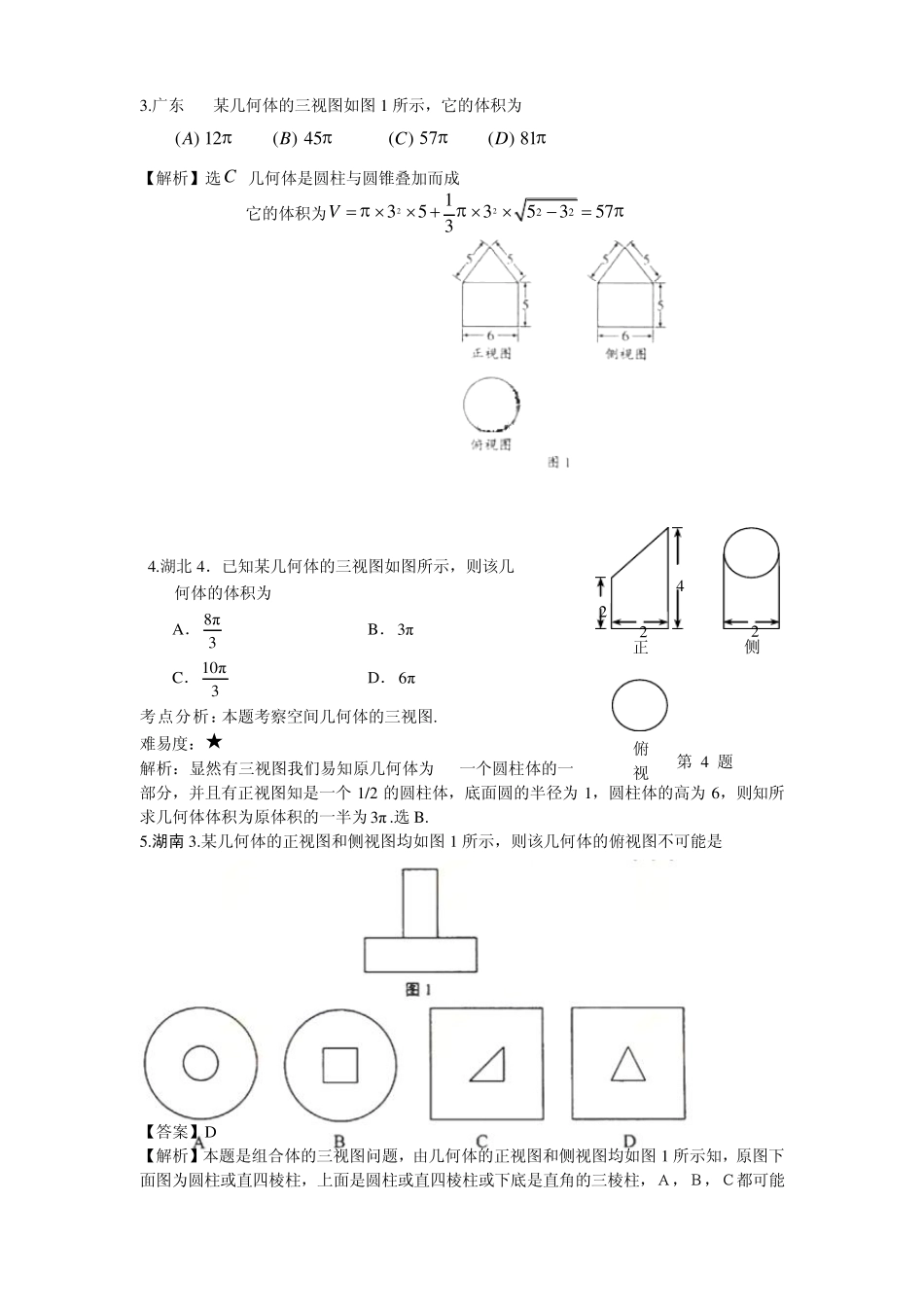
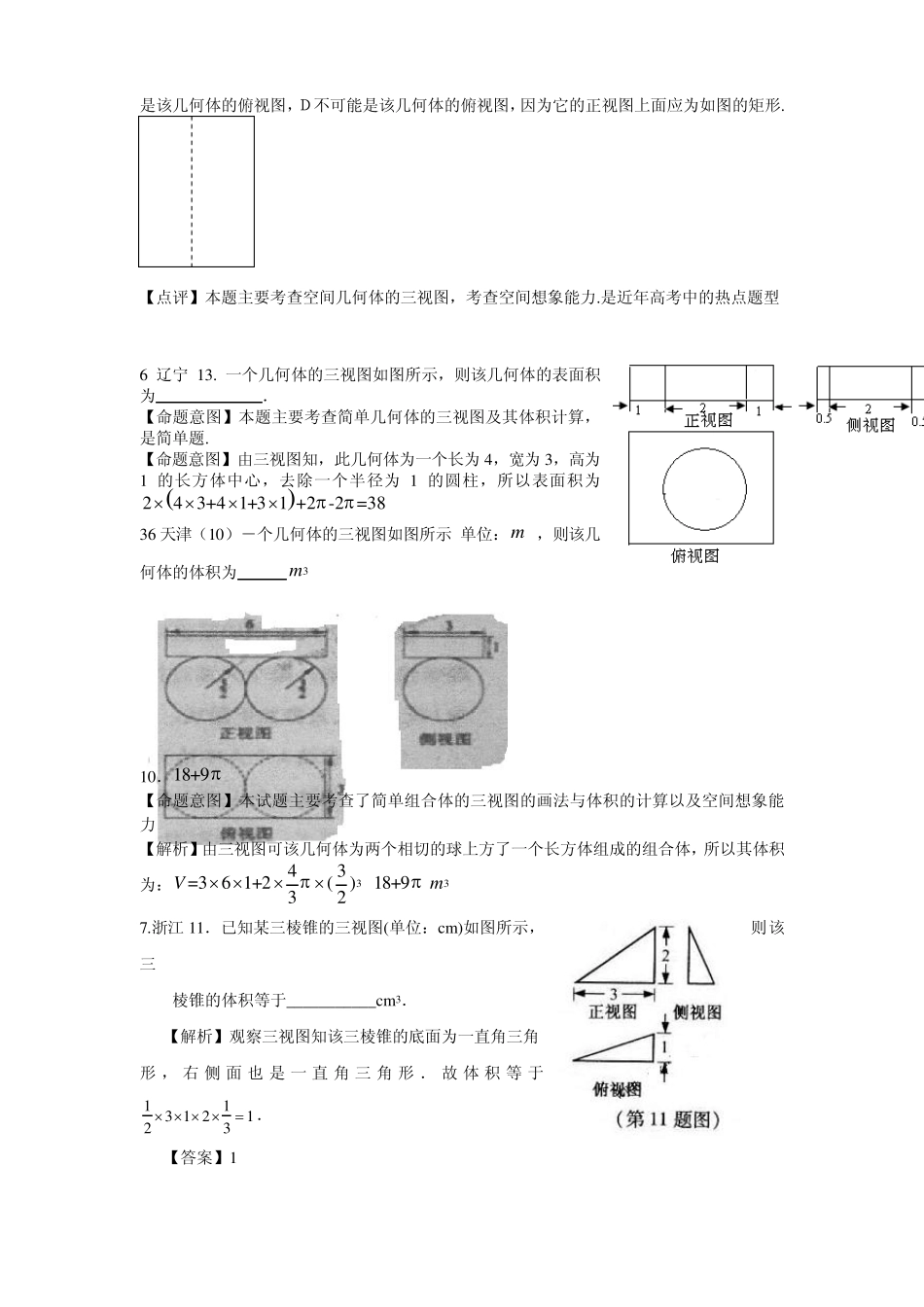
立体几何之三视图问题 1. (安徽12)某几何体的三视图如图所示,该几何体的表面积是_____ 【解析】表面积是_____ 92 该几何体是底面是直角梯形,高为4 的直四棱柱 几何体的表面积是2212(25)4(2544(52) ) 4922S 2.北京7.某三棱锥的三视图如图所示,该三梭锥的表面积是( ) A. 28+6 5 B. 30+6 5 C. 56+ 12 5 D. 60+12 5 【解析】从所给的三视图可以得到该几何体为三棱锥,如图所示,图中蓝色数字所表示的为直接从题目所给三视图中读出的长度,黑色数字代表通过勾股定理的计算得到的边长。本题所求表面积应为三棱锥四个面的面积之和,利用垂直关系和三角形面积公式,可得:10底S, 10后S, 10右S,56左S,因 此 该几何体表面积5630 左右后底SSSSS,故选 B。 【答案】B 3.广东6. 某几何体的三视图如图1 所示,它的体积为( ) ( )A 12 ( )B 45 ( )C ( )D 【解析】选C 几何体是圆柱与圆锥叠加而成 它的体积为2222135353573V 4.湖北 4.已知某几何体的三视图如图所示,则该几 何体的体积为 A. 8π3 B.3π C.10π3 D.6π 考点分析:本题考察空间几何体的三视图. 难易度:★ 解析:显然有三视图我们易知原几何体为 一个圆柱体的一部分,并且有正视图知是一个 1/2 的圆柱体,底面圆的半径为1,圆柱体的高为6,则知所求几何体体积为原体积的一半为3π .选 B. 5.湖南 3.某几何体的正视图和侧视图均如图1 所示,则该几何体的俯视图不可能是 【答案】D 【解析】本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1 所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C都可能俯视侧2 正第 4 题4 2 2 是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形. 【点评】本题主要考查空间几何体的三视图,考查空间想象能力.是近年高考中的热点题型 6 辽宁13. 一个几何体的三视图如图所示,则该几何体的表面积为 . 【命题意图】本题主要考查简单几何体的三视图及其体积计算,是简单题. 【命题意图】由三视图知,此几何体为一个长为4,宽为3,高为1 的长方体中心,去除一个半径为1 的圆柱,所以表面积为24 3+4 1+3 1 +2 -2 =38 36 天津(10)―个几何体的三视图如图所...