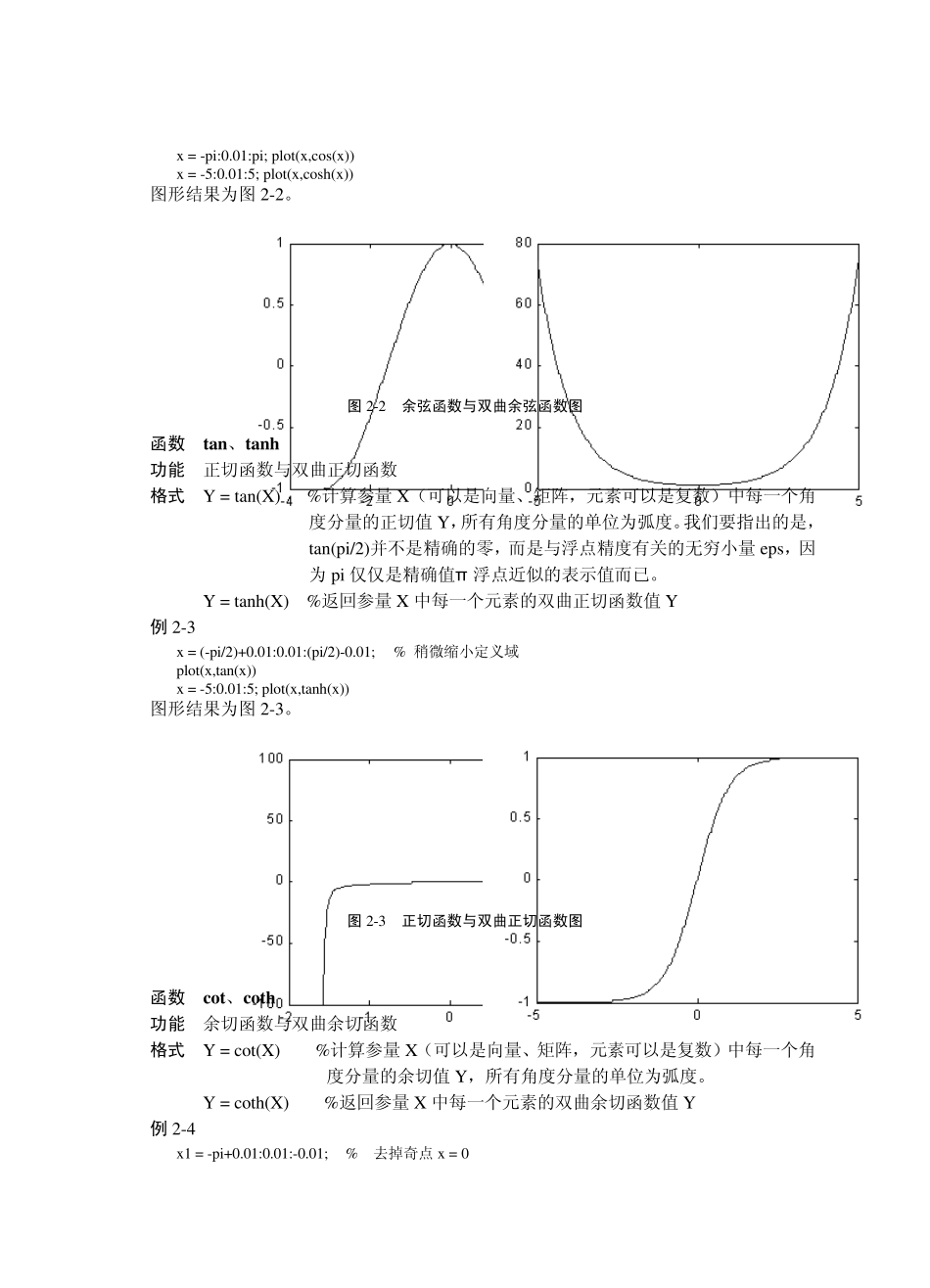
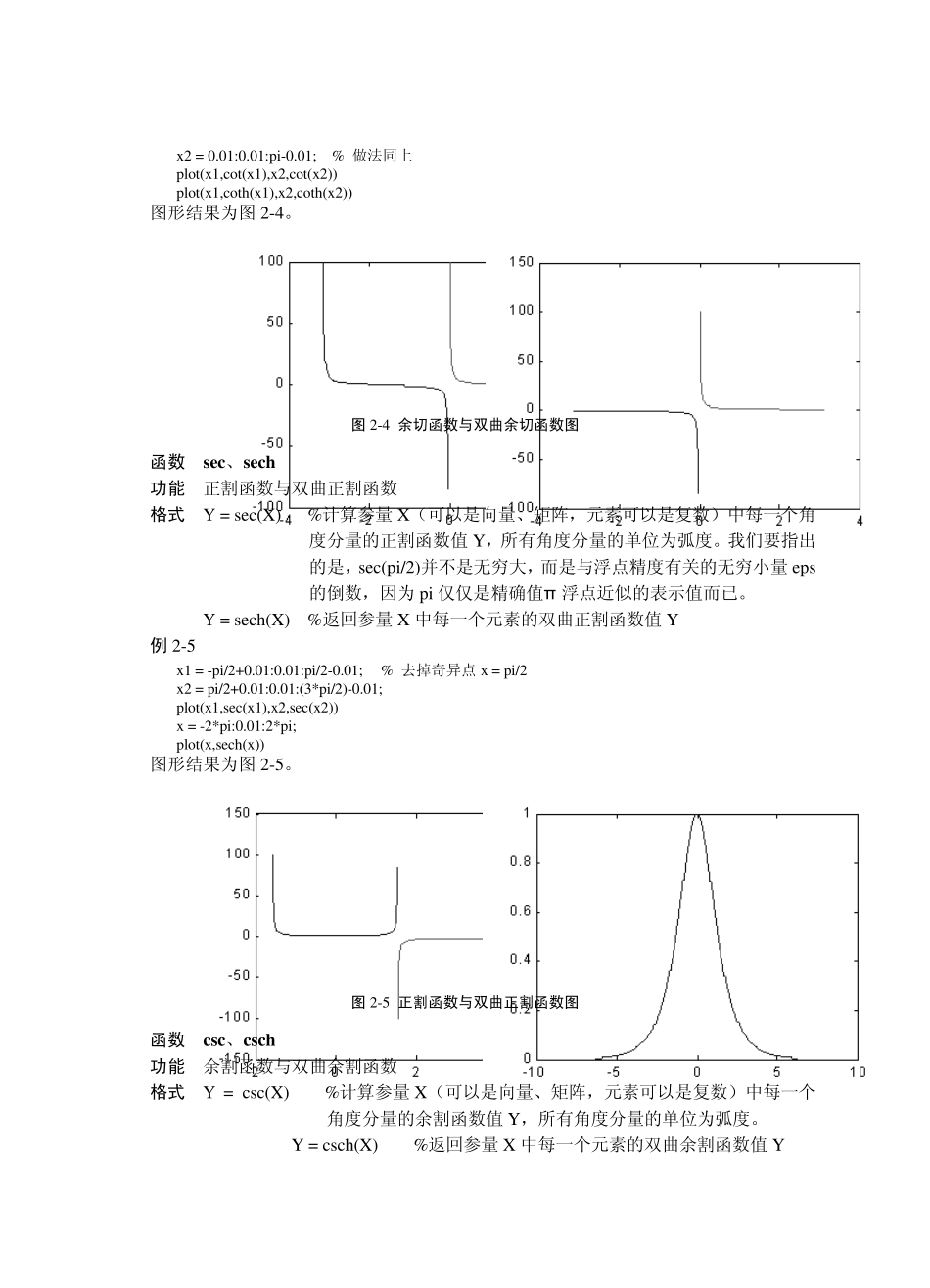
第2 章 数值计算与数据分析 2.1 基本数学函数 2.1.1 三角函数与双曲函数 函数 sin、sinh 功能 正弦函数与双曲正弦函数 格式 Y = sin(X) %计算参量 X 中每一个角度分量的正弦值Y,所有分量的角度单位为弧度。 Y = sinh(X) %计算参量 X 的双曲正弦值Y 注意:sin(pi)并不是零,而是与浮点精度有关的无穷小量eps,因为pi 仅仅是精确值π浮点近似的表示值而已 例2-1 x = -pi:0.01:pi; plot(x ,sin(x )) x = -5:0.01:5; plot(x ,sinh(x )) 图形结果为图 2-1。 图2-1 正弦函数与双曲正弦函数图 函数 cos、cosh 功能 余弦函数与双曲余弦函数 格式 Y = cos(X) %计算参量 X 中每一个角度分量的余弦值Y,所有角度分量的单位为弧度。我们要指出的是,cos(pi/2)并不是精确的零,而是与浮点精度有关的无穷小量 eps,因为 pi 仅仅是精确值π 浮点近似的表示值而已。 Y = sinh(X) %计算参量 X 的双曲余弦值Y 例2-2 x = -pi:0.01:pi; plot(x ,cos(x )) x = -5:0.01:5; plot(x ,cosh(x )) 图形结果为图2-2。 图2-2 余弦函数与双曲余弦函数图 函数 tan、tanh 功能 正切函数与双曲正切函数 格式 Y = tan(X) %计算参量 X(可以是向量、矩阵,元素可以是复数)中每一个角度分量的正切值 Y,所有角度分量的单位为弧度。我们要指出的是,tan(pi/2)并不是精确的零,而是与浮点精度有关的无穷小量 eps,因为pi 仅仅是精确值π 浮点近似的表示值而已。 Y = tanh(X) %返回参量 X 中每一个元素的双曲正切函数值 Y 例 2-3 x = (-pi/2)+0.01:0.01:(pi/2)-0.01; % 稍微缩小定义域 plot(x ,tan(x )) x = -5:0.01:5; plot(x ,tanh(x )) 图形结果为图2-3。 图2-3 正切函数与双曲正切函数图 函数 cot、coth 功能 余切函数与双曲余切函数 格式 Y = cot(X) %计算参量 X(可以是向量、矩阵,元素可以是复数)中每一个角度分量的余切值 Y,所有角度分量的单位为弧度。 Y = coth(X) %返回参量 X 中每一个元素的双曲余切函数值 Y 例 2-4 x 1 = -pi+0.01:0.01:-0.01; % 去掉奇点 x = 0 x 2 = 0.01:0.01:pi-0.01; % 做法同上 plot(x 1,cot(x 1),x 2,cot(x 2)) plot(x 1,coth(x 1),x 2,coth(x 2)) 图形结果为图2-4。 图2-4 余切函数与双曲余切函数图 函数 sec、sech 功能 正割函数与双曲正割函数 格式 Y = se...