第8章图的基本概念

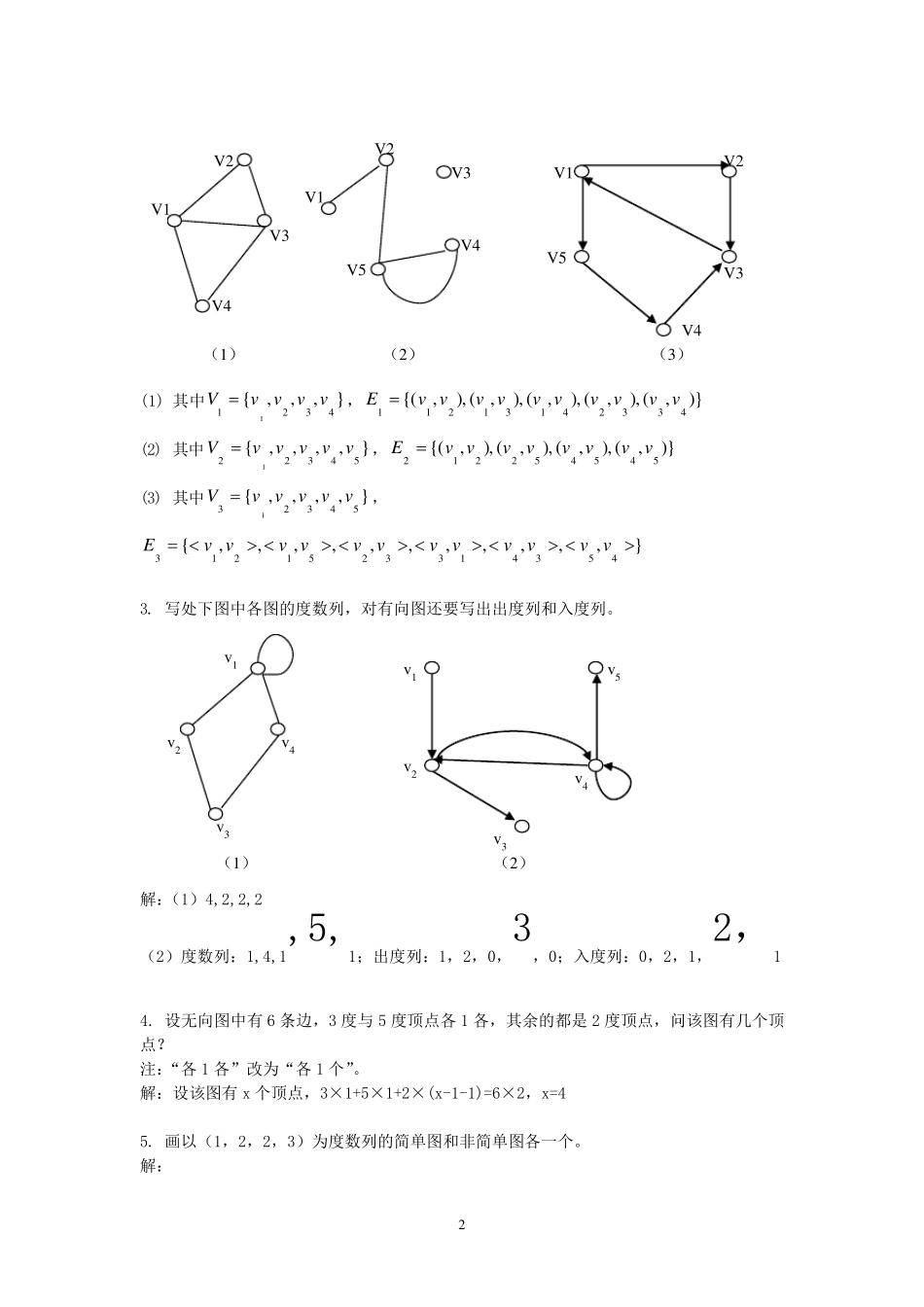
1 习题 8 1. 给定下面两个图的集合表示，画出他们的图形表示。 111, EVG, 其中},,,,{543211vvvvvV ，)},(),,(),,(),,(),,{(43415351211vvvvvvvvvvE  222, EVD, 其中},,,,{543221vvvvvV ，},,,,,,,,,{43412552212vvvvvvvvvvE 注：2D 改为2G 解： 2. 先将下图中各图的顶点标定次序，然后写出各图的集合表示。 解：顶点标定如下： 图G1 图G2 V1 V2 V3 V4 V5 V1 V2 V3 V4 V5 （1） （2） （3） 2 (1) 其中},,,{43211vvvvV ，)},(),,(),,(),,(),,{(43324131211vvvvvvvvvvE  (2) 其中},,,,{543221vvvvvV ，)},(),,(),,(),,{(545452212vvvvvvvvE  (3) 其中},,,,{543231vvvvvV ，},,,,,,,,,,,{4534133251213vvvvvvvvvvvvE 3. 写处下图中各图的度数列，对有向图还要写出出度列和入度列。 解：（1）4,2,2,2 （2）度数列：1,4,1,5,1；出度列：1，2，0，3，0；入度列：0，2，1，2，1 4. 设无向图中有6 条边，3 度与5 度顶点各1 各，其余的都是2 度顶点，问该图有几个顶点？ 注：“各1 各”改为“各1 个”。 解：设该图有x 个顶点，3×1+5×1+2×(x-1-1)=6×2，x=4 5. 画以（1，2，2，3）为度数列的简单图和非简单图各一个。 解： （1） （2） （3） V1 V1 V1 V2 V2 V2 V3 V3 V3 V4 V4 V4 V5 V5 （1） （2） v1 v3 v4 v1 v2 v3 v4 v5 v2 3 6．证明在任何有向完全图中，所有结点入度的平方之和等于所有结点的出度平方之和。 证明：设有向完全图有n 个结点v1, v2,…, vn， 结点vi 的入度为 d-(vi)=n-1，出度为 d+(vi)=n-1， 所有结点入度的平方之和为21122i-1-n1-n)(vdninin， 所有结点出度的平方之和为21122i1-n1-n)(vdninin， 故所有结点入度的平方之和等于所有结点的出度平方之和。 7．写出下图相对于完全图的补图。 解： 8．证明下图中的两个图不同构。 4 证明：将图的顶点标定如下： 如果这两个图同构，那么对应结点的度数应相同。度数为3 的两个结点v1与v1'相对应。但与v1邻接的三个结点中一个结点v2度数为2 ，两个结点v3 ,v4度数为1 ，而与v1'邻接的三个结点中有两个结点v2',v3'度数为2 ，一个结点v4'度数为1 ，故他们不同构。 9．一个图如果同构于它的补图，则该图称为自补图。 1）试给出一...