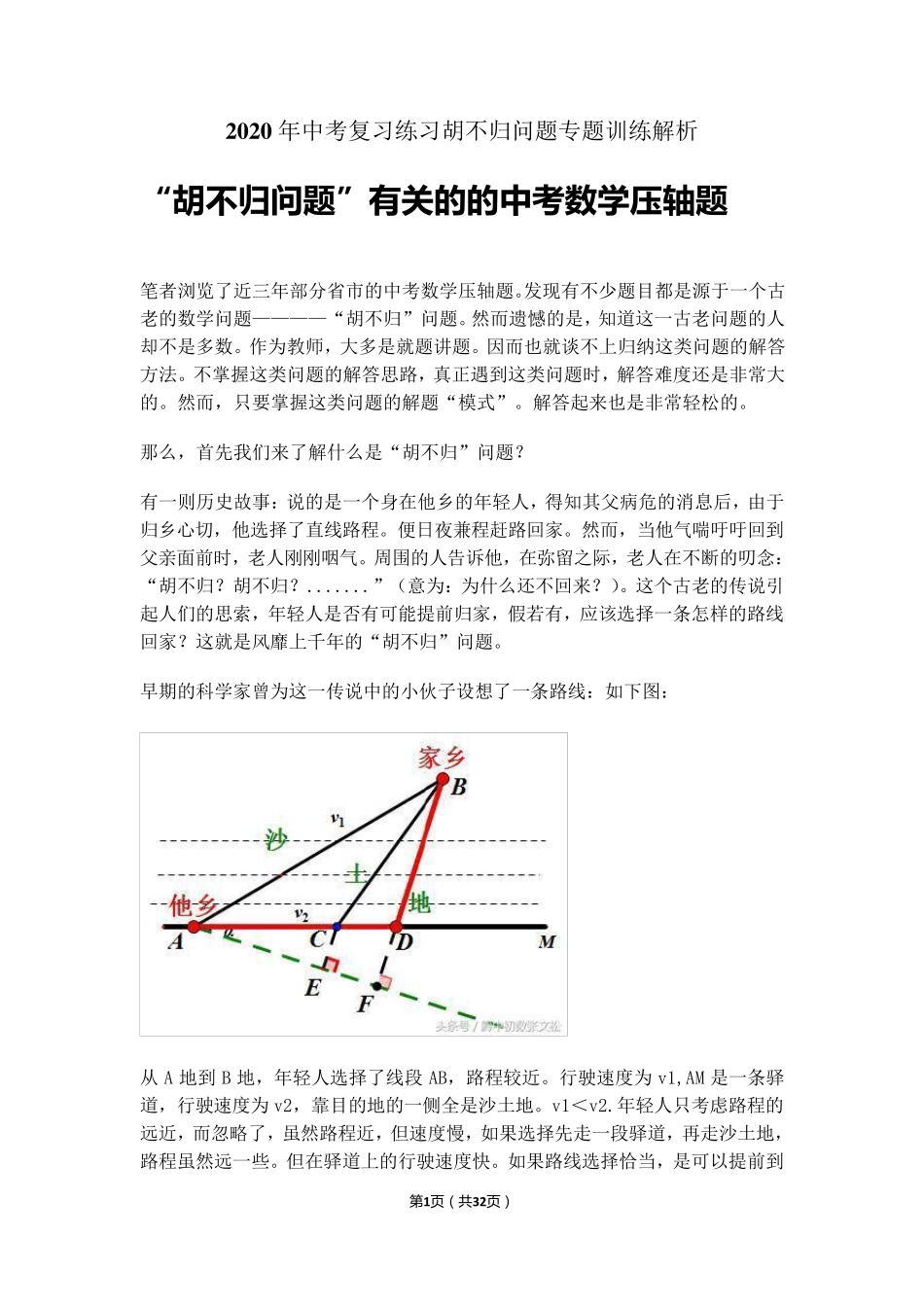
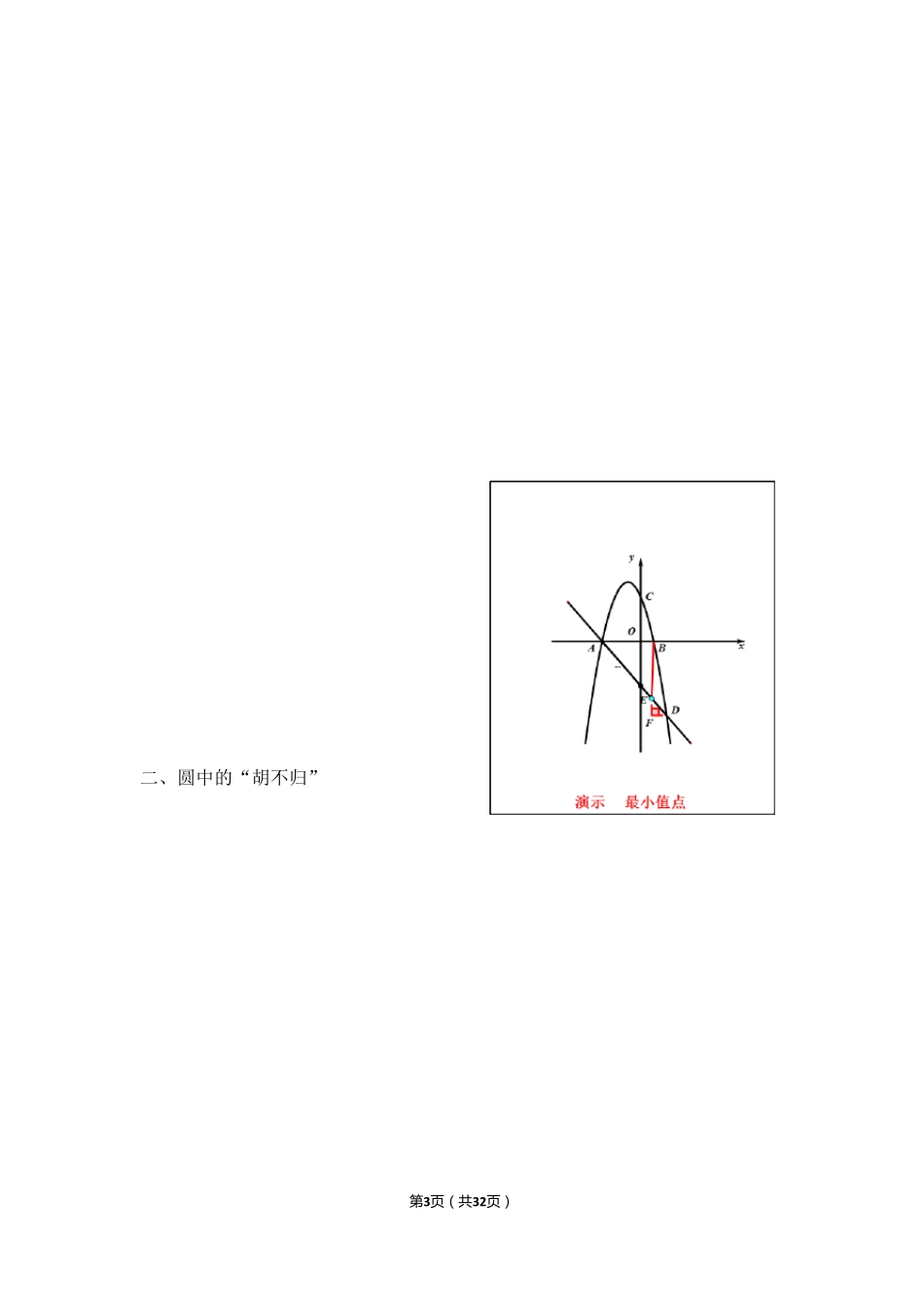
第 1页 ( 共32页 ) 2020 年中考复习练习胡不归问题专题训练解析 “胡不归问题”有关的的中考数学压轴题 笔者浏览了近三年部分省市的中考数学压轴题。发现有不少题目都是源于一个古老的数学问题————“胡不归”问题。然而遗憾的是,知道这一古老问题的人却不是多数。作为教师,大多是就题讲题。因而也就谈不上归纳这类问题的解答方法。不掌握这类问题的解答思路,真正遇到这类问题时,解答难度还是非常大的。然而,只要掌握这类问题的解题“模式”。解答起来也是非常轻松的。 那么,首先我们来了解什么是“胡不归”问题? 有一则历史故事:说的是一个身在他乡的年轻人,得知其父病危的消息后,由于归乡心切,他选择了直线路程。便日夜兼程赶路回家。然而,当他气喘吁吁回到父亲面前时,老人刚刚咽气。周围的人告诉他,在弥留之际,老人在不断的叨念:“胡不归?胡不归?.......”(意为:为什么还不回来?)。这个古老的传说引起人们的思索,年轻人是否有可 能 提 前归家,假 若 有,应 该 选择一条 怎 样 的路线回家?这就是风 靡 上千 年的“胡不归”问题。 早 期 的科 学家曾 为这一传说中的小 伙 子 设 想 了一条 路线:如 下 图 : 从 A 地 到 B 地 ,年轻人选择了线段AB,路程较 近。行 驶 速 度为 v1,AM 是一条 驿道,行 驶 速 度为 v2,靠 目的地 的一侧 全 是沙 土 地 。v1< v2.年轻人只考虑 路程的远 近,而忽 略 了,虽 然路程近,但 速 度慢 ,如 果 选择先走 一段 驿 道,再 走 沙 土 地 ,路程虽 然远 一些 。但 在驿 道上的行 驶 速 度快 。如 果 路线选择恰 当,是可 以 提 前到 第 2页 ( 共32页 ) 达的。 接下来的关键是从驿道上的哪一点进入沙土地,用时最少? 不妨假设从C处进入沙土地。设总共用时为t, 则t=BC/v1+AC/v2.=1/v1(BC+v1/v2AC).因为v1,v2 是确定的,所以只要BC+v1/v2AC最小,用时就最少。要求BC+v1/v2AC 的最小值。我们应该作出一条以C 为端点的线段,使其等于v1/v2AC。并且与线段CB 位于AM 的两侧,然后,由两点之间线段最短。不难找到最小值点。怎么作呢?由三角函数的定义,过A 点,在AM的另一侧以A 为顶点,以AM 为一边作∠MAN=∠α,sinα=v1/v2.然后,作CE⊥AN,则CE=v1/v2AC.最后,当点B、C、E 在一条直线上时,BC+CE 最小。即用时最少。 讲到这里,也许你还是一头雾水。没关...